Wie erstelle ich ein Funktionsterm für eine halbe Parabel

Question

Upload failed: [object Object]Aufgabe: auf eine PKW Teststrecke geht die Höchstgeschwindigkeit von 130 km/h. Bei einem Test Pkw wurde verschiedenen Geschwindigkeiten. V zwischen 20 km/h und 100 km/h gemessen, wie lange die zugehörige Bremsweg s ist.

Tabelle: oben:Geschwindigkeit v in km/h

           Unten: Länge s des Bremsweges in m

20	40	60	80	100
4	14	33	55	88

a. stellen Sie die Messergebnisse aus der Tabelle im Koordinatensystem grafisch. Da ermitteln Sie ein passendes Funktionsterm, der die Messergebnisse modelliert.

b. berechnen Sie mithilfe des Funktions Terms für weitere Geschwindigkeiten die Länge des zugehörigen Bremsweges. Wie lang kann bei diesem Test Pkw der Bremsweg auf der Test Strecke höchstens sein.

Problem/Ansatz:

Wenn man die Tabelle auswertet und in ein Koordinatensystem einzeichnet erkennt man das es eine halbe Parabel ist. Ich komme einfach nicht weiter welchen Ansatz ich benutzen soll um ein Funktionsterm zu erstellen für so eine "halbe“ Parabel. Muss ich dafür die normale Form: a mal hoch 2 +b verwenden oder wie soll ich hier starten.

Comments

Welche Methode hab ihr denn kennengelernt zur Bearbeitung der Aufgaben zu

Regressionsrechnung/Kurvenfitten/Ausgleichskurve...

---

Wir wiederholen zurzeit nur Funktionen und aufstellen von Gleichungen. Scheitelpunktform,allgm Formel etc. Regressionen haben wir noch nicht angefangen

Answer 1

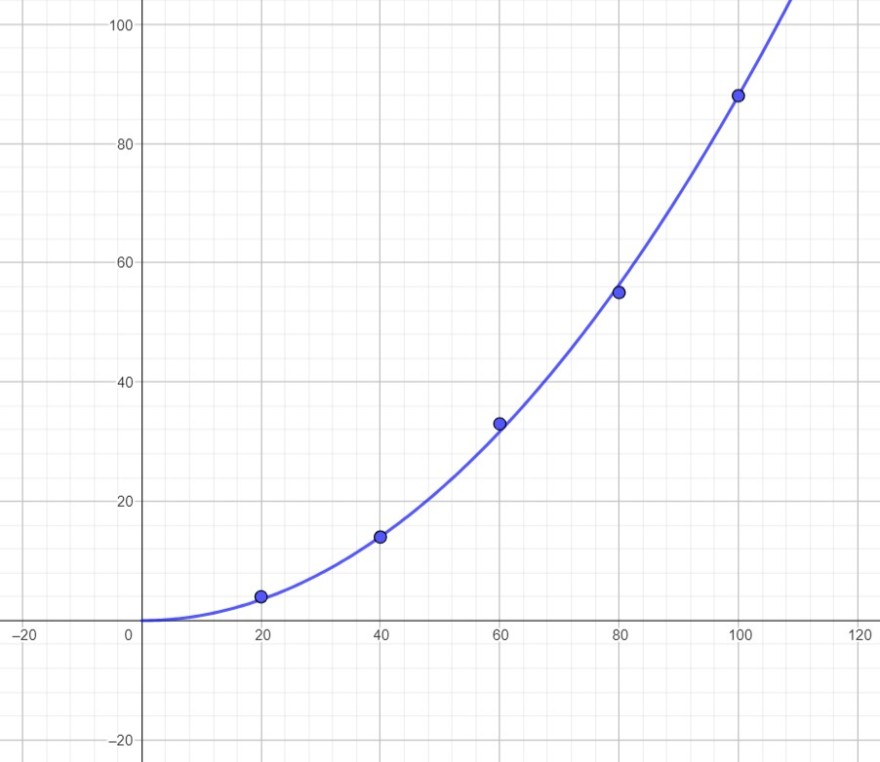
Wir vermuten einen Funktionsterm

s = a * v²

Ich benutze den Punkt (100 | 88) um a zu ermitteln.

88 = a * 100² --> a = 0.0088

Jetzt macht man eine Wertetabelle, um die anderen Punkte zu prüfen.

[v, 0.0088 * v²;
20, 3.52;
40, 14.08;
60, 31.68;
80, 56.32;
100, 88]

Man sieht das die Punkte für die Geschwindigkeiten 60 und 80 gerundet nicht richtig sind. Das kann man in Kauf nehmen. Ansonsten kann man auch ein Näherungspolynom berechnen.

Eine Halbe Parabel bekomme ich indem ich den Definitionsbereich für v auf Werte größer oder gleich Null beschränke.

Comments

Mann könnte auch eine Parabel nehmen unter der alle Punkte liegen um so den maximalen Bremsweg bei 130 km/h abschätzen zu können.

Answer 2

Dann würde ich ggf. alle Funktionen aufstellen

X: je aus Tabelle

Y:

Y(k) / (X(k))² x², k=1, 5

$\small p_{1..5}(x) \, := \, \left\{ \frac{1}{100} \; x^{2}, \frac{7}{800} \; x^{2}, \frac{11}{1200} \; x^{2}, \frac{11}{1280} \; x^{2}, \frac{11}{1250} \; x^{2} \right\}$

$\small p_{1..5}(130)= \left\{ 169, 147.875, 154.917, 145.234, 148.72 \right\}$

also max ca. 169m