Wie bekomme ich die Smith Normal Form?

Question

Aufgabe:

Wie bekomme ich die Smith Normal Form

Problem/Ansatz:

Es gibt einen Schritt den ich nicht verstehe und zwar derjenige bei dem man den ggT bestimmt und alle anderen Einträge der Spalte modifiziert. Hier ein Beispiel von Wikipedia: https://en.wikipedia.org/wiki/Smith_normal_form

Text erkannt:

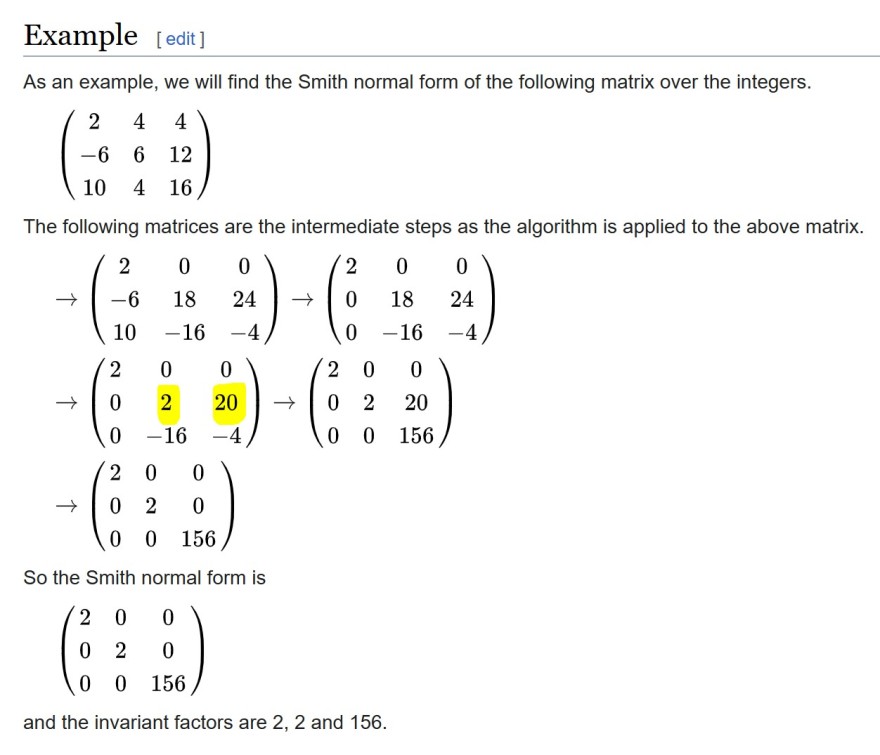
Example [edit]
As an example, we will find the Smith normal form of the following matrix over the integers.
$\left(\begin{array}{ccc} 2 & 4 & 4 \\ -6 & 6 & 12 \\ 10 & 4 & 16 \end{array}\right)$

The following matrices are the intermediate steps as the algorithm is applied to the above matrix.
$\begin{array}{l} \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ -6 & 18 & 24 \\ 10 & -16 & -4 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 18 & 24 \\ 0 & -16 & -4 \end{array}\right) \\ \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 20 \\ 0 & -16 & -4 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 20 \\ 0 & 0 & 156 \end{array}\right) \\ \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 156 \end{array}\right) \end{array}$

So the Smith normal form is
$\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 156 \end{array}\right)$
and the invariant factors are 2, 2 and 156 .

Nun verstehe ich das gelb Makierte nicht. Der ggt von 18 und -16 ist 2 okay. Aber wie wird aus 24 20? Dasselbe Problem hier: https://de.wikipedia.org/wiki/Smith-Normalform

Text erkannt:

Als Beispiel wird die Smith-Normalform der Matrix
$A=\left(\begin{array}{ccc} 2 & 4 & 4 \\ -6 & 6 & 12 \\ 10 & -4 & -16 \end{array}\right)$
berechnet. Die folgenden Matrizen sind die Zwischenschritte des Smith-Algorithmus angewandt auf diese Matrix:
$\begin{array}{l} \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ -6 & 18 & 24 \\ 10 & -24 & -36 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 18 & 24 \\ 0 & -24 & -36 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 18 & 24 \\ 0 & -6 & -12 \end{array}\right) \\ \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 6 & 12 \\ 0 & 18 & 24 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 6 & 12 \\ 0 & 0 & -12 \end{array}\right) \rightarrow\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 12 \end{array}\right) \end{array}$

Die letzte Matrix stellt dann die Smith-Normalform von $A$ dar. Die invarianten Faktoren von $A$ sind damit 2,6 und 12 .

Der ggT von 18 und -24 ist 6. Aber woher kommt die 12?

Vielen Dank für eure Hilfe

Answer 1

Aber wie wird aus 24 20?

Man hat zur zweiten Zeile

0    18    24

die dritte Zeile

0   -16   -4

addiert.

Comments

Okay, das war wohl einfacher als Gedacht... danke