Hilfe bei Geometrie-Aufgabe?

Question

Aufgabe:

Hallo, ich bräuchte Hilfe bei der Teilaufgabe c).

Vielen Dank schonmal im Voraus :)

Problem/Ansatz:

Die Teilaufgaben a) und b) habe ich bereits. Allerdings weiß ich bei c) nicht mehr weiter.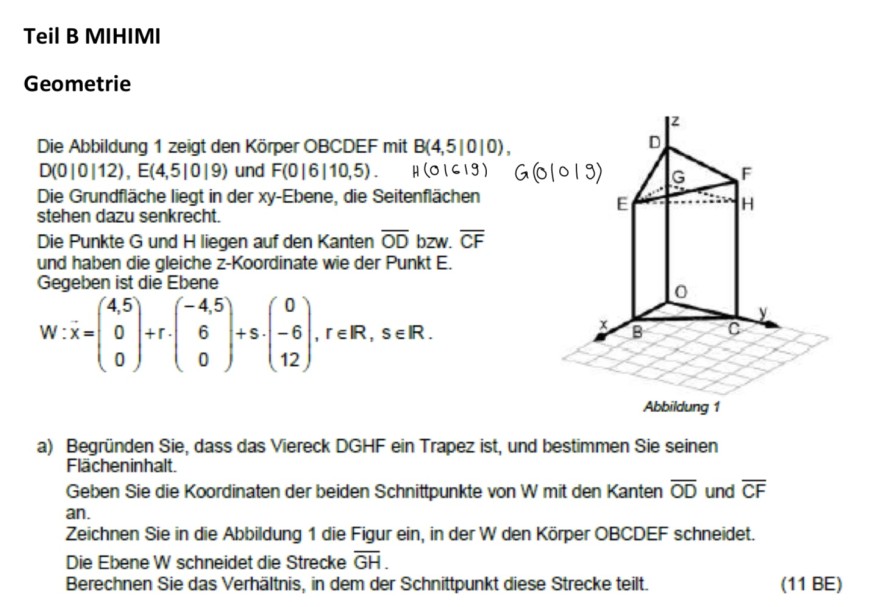

Text erkannt:

Teil B MIHIMI
Geometrie

Die Abbildung 1 zeigt den Körper OBCDEF mit $\mathrm{B}(4,5|0| 0)$, $D(0|0| 12), E(4,5|0| 9)$ und $F(0|6| 10,5)$. $\quad H(0|6| 9)$ Die Grundfläche liegt in der xy-Ebene, die Seitenflächen stehen dazu senkrecht.
Die Punkte $\mathrm{G}$ und $\mathrm{H}$ liegen auf den Kanten $\overline{\mathrm{OD}}$ bzw. $\overline{\mathrm{CF}}$ und haben die gleiche $z$-Koordinate wie der Punkt $E$. Gegeben ist die Ebene
$W: \vec{x}=\left(\begin{array}{c} 4,5 \\ 0 \\ 0 \end{array}\right)+r \cdot\left(\begin{array}{c} -4,5 \\ 6 \\ 0 \end{array}\right)+s \cdot\left(\begin{array}{c} 0 \\ -6 \\ 12 \end{array}\right), r \in \mathbb{R}, s \in \mathbb{R} \text {. }$
a) Begründen Sie, dass das Viereck DGHF ein Trapez ist, und bestimmen Sie seinen Flächeninhalt.
Geben Sie die Koordinaten der beiden Schnittpunkte von W mit den Kanten $\overline{\mathrm{OD}}$ und $\overline{\mathrm{CF}}$ an.
Zeichnen Sie in die Abbildung 1 die Figur ein, in der W den Körper OBCDEF schneidet.
Die Ebene W schneidet die Strecke $\overline{\mathrm{GH}}$.
Berechnen Sie das Verhältnis, in dem der Schnittpunkt diese Strecke teilt.
(11 BE)

Text erkannt:

b) Der Punkt $M\left(m_{1}\left|m_{2}\right| 0\right)$ hat von allen Seiten des Dreiecks OBC den gleichen Abstand. Begründen Sie, dass $m_{1}=m_{2}$ gilt.
Die Gleichungen (I) und (II) liefern gemeinsam einen Ansatz zur Bestimmung der Koordinaten des Punktes M:
(I) $([\overrightarrow{O B}+r \cdot \overrightarrow{B C}]-\overrightarrow{O M}) \cdot \overrightarrow{B C}=0$
(II) $|[\overline{\mathrm{OB}}+\mathrm{r} \cdot \overrightarrow{\mathrm{BC}}]-\overline{\mathrm{OM}}|=\mathrm{m}_{1}$
Stellen Sie die Bedeutung der beiden Gleichungen im xy-Koordinatensystem in Abbildung 2 dar.
(7 BE)

Betrachtet werden die Geraden $g_{u}: \vec{x}=\left(\begin{array}{c}4,5 \\ 0 \\ 0\end{array}\right)+t \cdot\left(\begin{array}{c}-4,5 \\ 6-6 u \\ 12 u\end{array}\right), u \in \mathbb{R}, t \in \mathbb{R}$.
c) Ermitteln Sie diejenigen Werte von $u$, für die $g_{u}$ die $x y$-Ebene jeweils unter einem Winkel der Größe $30^{\circ}$ schneidet.
Begründen Sie, dass die folgende Aussage falsch ist: Jeder Punkt der Ebene W liegt auf einer der Geraden $\mathrm{g}_{\mathrm{u}}$.
$(6 \mathrm{BE})$

Answer 1

Der Normalenvektor $\vec{n}$ der xy-Ebene ist $\begin{pmatrix} 0\\0\\1 \end{pmatrix}$. Der Richtungsvektor $\vec{r}$  der Geraden g_u ist in Abhängigkeit von u gegeben. $\vec{n}$ und $\vec{r}$ sollen einen Winkel von 60° bilden, damit die Gerade g_u mit der xy-Ebene einen Winkel von 30° bildet.

Answer 2

c)

Winkel zwischen einer Geraden und einer Ebene

SIN(30°) = ABS([-4.5, 6 - 6·u, 12·u]·[0, 0, 1])/(ABS([-4.5, 6 - 6·u, 12·u])·1) --> u = - √291/44 - 1/11 ∨ u = √291/44 - 1/11

Der Punkt [4.5, 0, 0] + [0, -6, 12] liegt nicht auf gu. Kannst du begründen warum nicht?

Comments

Leider kann ich das nicht begründen, vielleicht kannst du mir das erklären und vielleicht auch wie du auf die Punkt kommst?

---

In der Ebene kannst du s unabhängig von r verändern. D.h. r kann 0 und s kann 1 sein. Das ist daher ein Punkt von der Ebene W.

In der Geradengleichung kann ich zwar t = 0 wählen aber damit sind automatisch auch die Terme die u enthalten Null und die können jetzt nicht unabhängig einen anderen Wert bekommen.

Daher liegt der Punkt eben nicht auf der Geradenschaar gu.

---

Also irgendwie verstehe ich es immer noch nicht so ganz hast du dir die Punkte einfach überlegt?

---

Jaein.

Schau einfach mal wodurch sich die Ebenengleichung und die Geradenschaar unterscheiden.

gu: X = [4.5, 0, 0] + t·[-4.5, 6 - 6·u, 12·u]

gu: X = [4.5, 0, 0] + t·[-4.5, 6, 0] + t·u·[0, - 6, 12]

mit s = t·u ergibt sich also genau die Gleichung der Ebene. Nur das wenn t = 0 gewählt wird hier auch automatisch s = 0 gilt und s dann nicht unabhängig von t frei gewählt werden kann wie das in der Ebene der Fall ist.

---

Also ich möchte nicht nerven und finde es echt toll dass du mir antwortest und es versuchst mir zu erklären. Aber irgendwas verstehe ich daran immer noch nicht, vor allem wie man auch auf die Punkte kommt und warum man s durch t•u ersetzen kann?

---

Wenn du t*u durch s ersetzt ergibt sich doch die Gleichung der Ebene.

Siehst du das oder siehst du das nicht?

Wärend man in der Ebene Aber t = 0 und s = 1 wählen kann geht das in der Geradenschar nicht weil wenn ich für t = 0 wähle habe ich t = 0 und s = 0*u = 0

Ich kann also nicht t = 0 und s ≠ 0 wählen.

---

Nee, das sehe ich nicht

---

Nee, das sehe ich nicht

Dann bin ich raus. Tut mir leid.