Normalverteilung (Standardisierung) my, sigma

Question

Aufgabe: Berechnen Sie für die μ = 2 und σ = 5 normalverteilte Zufallsvariable X:

P(|X| ≥ 2) = ....

Frage: Wie löse ich so eine Darstellung am besten? Ich möchte mir das graphisch vorstellen können.

Ansatz:

Man braucht ja bestimmt eine lineare Rücktransformation:

Z = ((X - μ) / σ) = Z = ((2 - 2)/ 2) = 0

φ(0) = 0.5

Aber wie gehe ich weiter? Irgendwie muss ich das |X| >= 2 umschreiben, so dass man dann die Verteilungsfunktion der Standardnormalverteilung verwenden kann.

Bitte ganze Antworten und nicht nur Kommentare!

Comments

Meinst du dies?

Hier: f(x)=$\frac{1}{5\sqrt{2π}}$ ·$e^{\frac{1}{2}·(\frac{x-2}{5})^{2}}$.

---

Hallo Roland,

vielen Dank für deine Antwort.

Ja genau!

Answer 1

Aloha :)

Du hast hier eine Normalverteilung für die Zufallsvariable $X$ mit$$\mu=2\quad\text{und}\quad\sigma=5$$Die Gaußglocke hat also ihren höchsten höchsten Punkt bie $x=2$ und die beiden Wendepunkte liegen bei $x=-3$ und $x=7$. Unser Freund Wolfraum zeichnet sie so:

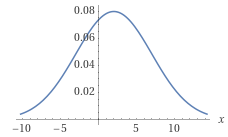
Die Wahrscheinlichkeit $P(|X|\ge2)$ deckt zwei Bereiche der Gaußglocke ab:$$P(|X|\ge2)=P(X\ge2)+P(X\le-2)$$Die Wahrscheinlichkeit $P(X\ge2)$ ist die Fläche unter der Gaußglocke vom höchten Punkt bei $x=2$ bis zu $x\to\infty$. Und die Wahrscheinlichkeit $P(X\le-2)$ ist die Fläche unter der Kurve von $x=-\infty$ bis $x=-2$.

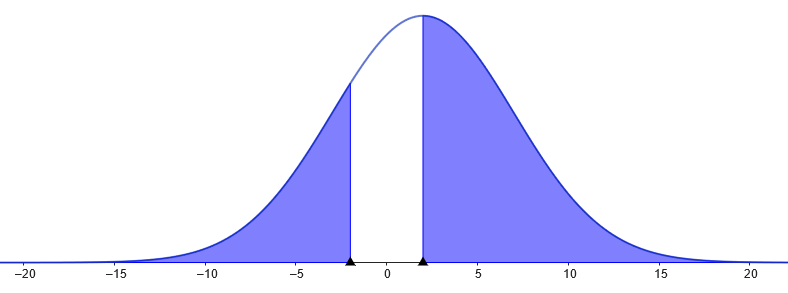
Berechnen kannst du das mit Hilfe der Standard-Normalverteilung $\phi(z)$. Sie gibt die Wahrscheinlichkeit an, dass eine standard-normalverteilte Zufallsvariable $Z$ einen Wert kleiner (oder gleich) $z$ hat:$$\phi(z)=P(Z\le z)\quad\text{wobei }\quad\mu_z=0\quad;\quad\sigma_z=1$$

Hier müsstest du also rechnen:$$P(|X|\ge2)=P(X\ge2)+P(X\le-2)=\left(1-P(X<2)\right)+P(X\le-2)$$$$\phantom{P(|X|\ge2)}=1-\phi\left(\frac{2-\mu}{\sigma}\right)+\phi\left(\frac{-2-\mu}{\sigma}\right)=1-\phi(0,5)+\phi(-0,8)$$$$\phantom{P(|X|\ge2)}\approx1-0,5+0,211855=0,711855$$

Wichtig ist hierbei die sogenannte "z-Transformation". Von dem Wert $x$ der Zufallsvariable wird der Erwartungswert $\mu$ subtrahiert, denn der Erwartungswert von $(x-\mu)$ ist Null. Dann wird noch durch die Standardabweichung dividiert, um sie auf den Wert $1$ zu normieren. Du baust dir sozusagen mittels$$z=\frac{x-\mu}{\sigma}$$eine standard-normalverteilte Zufallsvariable $z$ zusammen.

Answer 2

1 - P(-2 ≤ X ≤ 2) = 1 - 0.2881 = 0.7119

Comments

Das stimmt leider nicht...

Denn es gilt:

P(|X| ≥ 2) = 1- P(|X| < 2) = 1 - P(-2 < X < 2) = 0,7119

Du hast aber "≤"

---

Du hast aber "≤"

Das ist wie du weißt unerheblich, denn P(X = 2) ist exakt 0 und damit irrelavant, ob man die Wahrscheinlichkeit mit zählt oder nicht.

---

Woher weiß ich das P(x = 2) = 0 ist?

---

Woher weiß ich das P(x = 2) = 0 ist?

Das solltest du gelernt haben.

---

@cool

Im Fall einer stetigen Variable gilt stets P(X =x)=F(x)−F(x)=0,
d.h. für eine bel. feste Zahl x nimmt X den Wert x mit Wahrscheinlichkeit 0 an