Zeigen Sie, dass v1, v2, v3 linear unabhängig sind.

Question

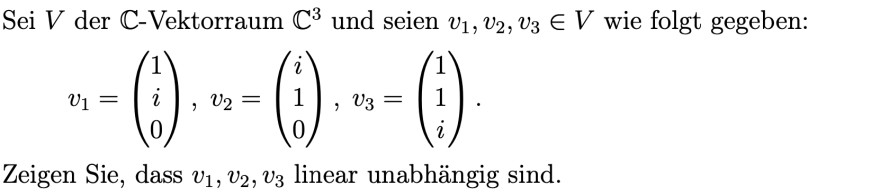
Text erkannt:

Sei $V$ der $\mathbb{C}$-Vektorraum $\mathbb{C}^{3}$ und seien $v_{1}, v_{2}, v_{3} \in V$ wie folgt gegeben:
$v_{1}=\left(\begin{array}{l} 1 \\ i \\ 0 \end{array}\right), v_{2}=\left(\begin{array}{l} i \\ 1 \\ 0 \end{array}\right), v_{3}=\left(\begin{array}{l} 1 \\ 1 \\ i \end{array}\right) .$

Zeigen Sie, dass $v_{1}, v_{2}, v_{3}$ linear unabhängig sind.

Muss ich hier gucken ob die Determinante ungleich Null ist oder für was das Gleichungssystem 0 ist?

Answer 1

Determinante ≠ 0 ist eine Möglichkeit.

Ich bekomme 2i.

Oder zeigen,

dass x*v1+y*v2+z*v3=0 mit x,y,z aus ℂ

als einzige Lösung x=y=z=0 hat.