Bestimmen Sie das Konfidenzintervall für den Erwartungswert

Question

Aufgabe:

Für eine neue Produktionsmethode wurden die in der Tabelle angegebenen Produktionsdauern $x_{i}$ in Minuten an einer Stichprobe im Umfang $n=12$ ermittelt. Es kann angenommen werden, dass die Produktionsdauer $\mathrm{X}$ normalverteilt ist, wobei $\mu$ und $\sigma$ unbekannt sind. Bestimmen Sie das Konfidenzintervall für den Erwartungswert $\mu$ mit einer Sicherheitswahrscheinlichkeit $\gamma=97 \%$.

Problem/Ansatz:

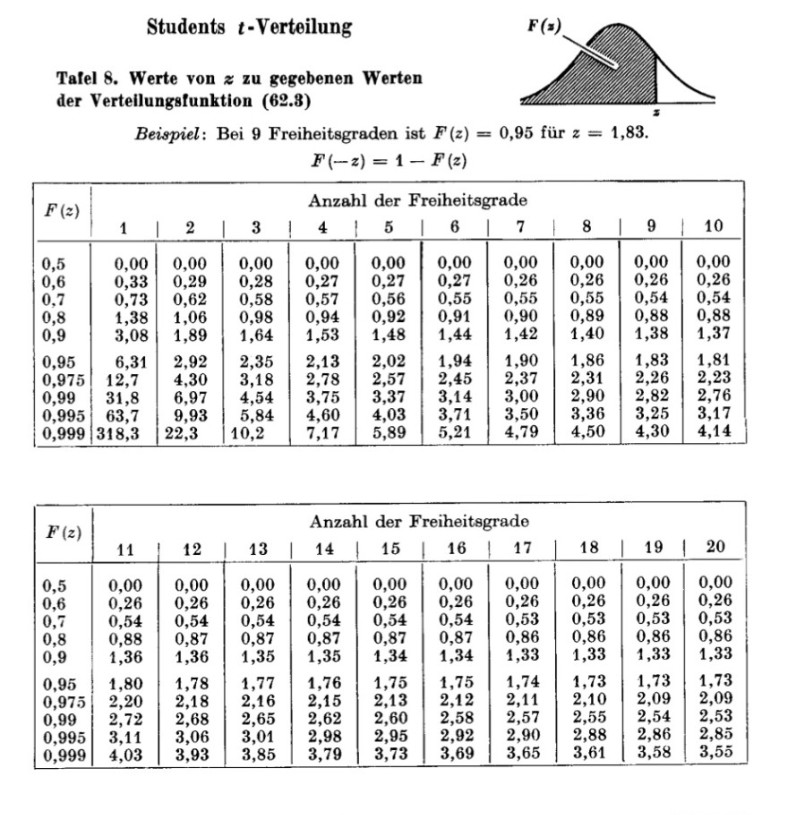
Den Durchschnitt habe ich mit 42,25 berechnet und die Standardabweichung s= 4,98. aus der t-Verteilung lese ich 2,72 ab.

Ich komme leider nicht auf die Lösung von P(38,42 ≤ μ ≤ 46.08)=97%.

ich komme auf P(38,33 ≤ μ ≤ 46.16)=97%.

wo könnte dieser kleiner Fehler liegen ?

Comments

In der Aufgabe geht es um 97 % und Du nennst den Tabellenwert für 99 %.

Bei der Standardabweichung komme ich auf 5,2071...

---

1-$\frac{1-0,97}{2}$= 0,985 und lese dann von 0,99 ab

---

Man sollte schon den richtigen t-Wert verwenden.

---

welcher t-Wert wäre denn dann richtig?

---

Ich komme auf 2,49 aber trotz aller Rundungsversuche nicht auf die von Dir genannte Musterlösung.