Ermitteln Sie, für welches a die Integralfunktionen Iₐ und l₀ zur Funktion g mit g(x) = 3x^2 + 4x identisch sind.

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x) = 4x^3.
a) Bestimmen Sie die Integralfunktionen I₋₂ und I₂ zu f und vergleichen Sie diese. Skizzieren Sie den Graphen von f und erklären Sie daran Ihre Beobachtung.

b) Ermitteln Sie, für welches a die Integralfunktionen Iₐ und l₀ zur Funktion g mit
g(x) = 3x^2 + 4x identisch sind.

Problem/Ansatz:

Hallo, kann mir jemand bei Teilaufgabe b) helfen? Irgendwie versteh ich das nicht ganz

was ich zu a) habe:

I₋₂(x)= x^4 - 16

I₂(x) = x^4 + 16 

Vielen Dank im Voraus!

Answer 1

Bei a) hast du einen Vorzeichenfehler: \(I_a(x) = \int_a^xf(t)\, dt = x^4-a^4\).

Damit ist \(I_{-2} = I_2\).

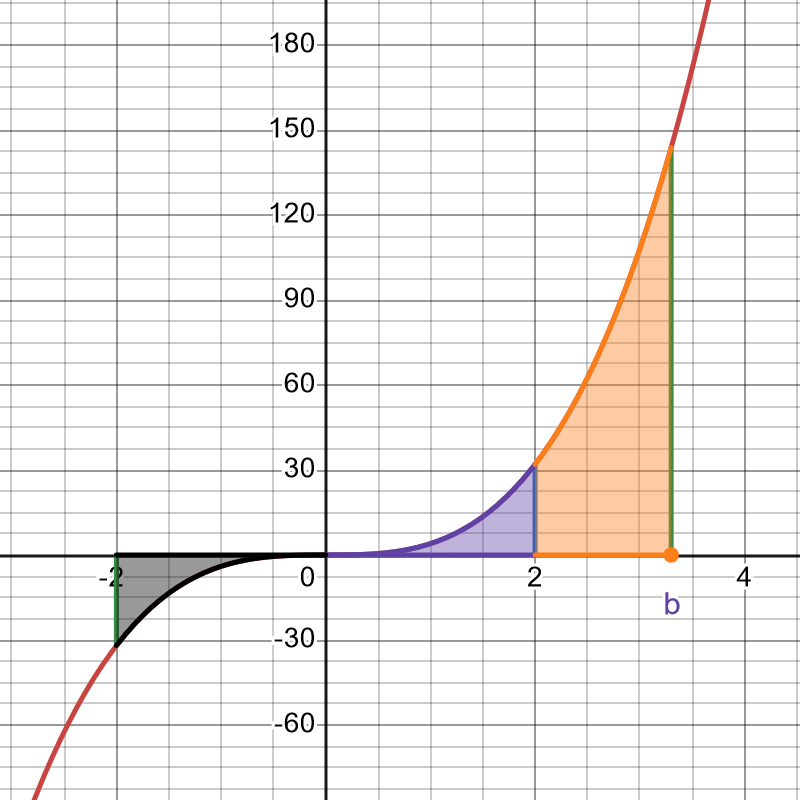
Hier eine kleine Illustration, die das verdeutlicht mit

\(I_{-2}(b) =b^4-(-2)^4 = b^4-2^4 = I_2(b) \):

Zu b)
Du integrierst zunächst einmal:
$$I_a(x)=\int_a^xg(t)\, dt = \int_a^x(3t^2+4t)\, dt= x^3+2x^2- (a^3+2a^2)$$Damit ist$$I_0(x) = x^3´+2x^2$$Nun sollst du ein \(a\) finden, sodass $$I_0(x) = I_a(x) \text{ für alle }x\in \mathbb R$$ Also$$a^3+2a^2 =a^2(a+2)\stackrel{!}{=}0\Rightarrow a=0 \text{ oder }\boxed{a=-2}$$