Zeigen Sie, dass die Graphen von f(x):=e^x-2 und g(x):=x^2-x genau eine Schnittstelle haben

Question

f,g:R->R durch        f(x):=e^x-2     und    g(x):=x^2-x.

Zeigen Sie,dass es genau ein psi gibt mit folgenden Eigenschaften

Zeigen Sie,dass es genau ein psi element der reellen zahlen gibt mit   f(psi)=g(psi)

Zeigen Sie, dass es genau ein ξ∈ℝ gibt mit f(ξ) = g(ξ).

Comments

f(x):=e^x-2     und    g(x):=x^2-x. ohne Klammern heisst, dass in

 f(x):=e^x - 2      und    g(x):=x^2 - x

jeweils nur x resp. nur 2 im Exponenten sind. Ist das so?

Im Graphen ist dann ersichtlich, dass sich f blau und g rot genau an einer Stelle schneiden.
Grün: f(x) - g(x) hat genau eine Nullstelle.
Man kann vermutlich zeigen, dass (f(x) - g(x)) ' > 0 für alle x in IR. Dann braucht's nur noch einen positiven und einen negativen Funktionswert. wegen der Stetigkeit weiss man dann, dass genau eine Nullstelle vorhanden ist.

Answer 1

 f(x) - g(x) =e^x - 2 - (x^2 - x) = e^x -x^2 + x - 2

(f(x) - g(x))' = e^x - 2x + 1  ist für x<0 immer ≥ o, da dann nur positive Summanden vorkommen.

Fall x>0

e^x - 2x + 1  

Gemäss Wikipedia Exponentialfunktion

e^x = 1+x + x^2/2! + x^3/3!+ .............

Also e^x - 2x + 1 = 1 + x +x^2/2! + x^3/3! +… - 2x +1 = 2-x + x^2/2 + x^3/3! + …

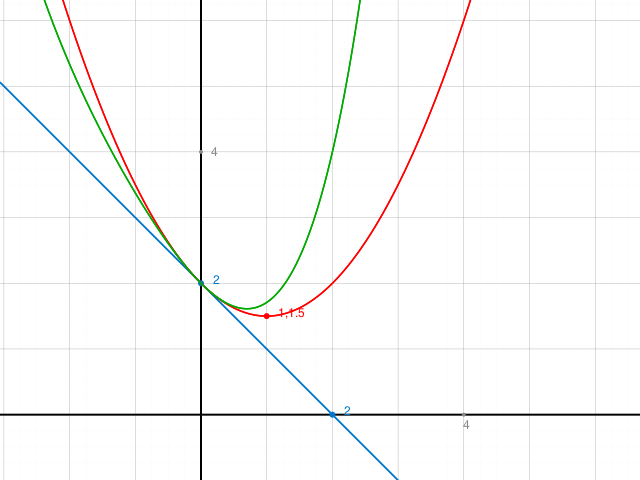
Betrachte die Skizze rechts von der y-Achse:

y = 2-x schneidet noch die x-Achse

y = 2-x+ x^2 / 2             Schon sind keine Funktionswerte < 0 mehr möglich.

Wenn nun weitere Summanden dazukommen, kann rechts der y-Achse kein x-Achsendurchstoss mehr vorkommen. 

qed gemäss meinem Kommentar zur Aufgabenstellung.

Im Graph noch das Bsp. (grün)

y =  2-x + x^2/2 + x^3/3! + x^4 / 4!