Wie berechne ich die Inverse Matrix mit b?

Question

Aufgabe:

Wie berechne ich die Inverse Matrix mit b?

Hier die Aufgabe:

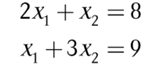
Text erkannt:

$\begin{array}{l}2 x_{1}+x_{2}=8 \\ x_{1}+3 x_{2}=9\end{array}$

Unten die A-1 also die inverse Matrix und die (8 und 9) sind anscheinend die B:

Ich habe in keinem Youtube Video gesehen, dass nachdem man die Inverse A-1 berechnet hat, nochmal irgendwie mit b verrechnet. Daher die Frage, wie berechne ich A-1 und B, um auf 3 und 2 zu kommen?

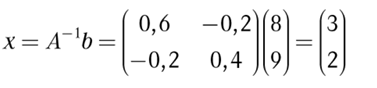
Text erkannt:

$x=A^{-1} b=\left(\begin{array}{cc}0,6 & -0,2 \\ -0,2 & 0,4\end{array}\right)\left(\begin{array}{l}8 \\ 9\end{array}\right)=\left(\begin{array}{l}3 \\ 2\end{array}\right)$

Answer 1

$$\begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix} \cdot \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 8\\9 \end{pmatrix} \newline \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix}^{-1} \cdot \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix} \cdot \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix}^{-1} \cdot \begin{pmatrix} 8\\9 \end{pmatrix} \newline \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix}^{-1} \cdot \begin{pmatrix} 8\\9 \end{pmatrix} \newline \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 0.6 & -0.2 \\ -0.2 & 0.4 \end{pmatrix} \cdot \begin{pmatrix} 8\\9 \end{pmatrix} \newline \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 0.6 \cdot 8 - 0.2 \cdot 9\\-0.2 \cdot 8 + 0.4 \cdot 9\end{pmatrix} \newline \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 3\\2 \end{pmatrix}$$

Comments

Ich finde solche Aufgaben richtig dämlich.

"Um das Gleichungssystem zu lösen, multipliziere es einfach mit der inversen Matrix."

Und wie findet man die inverse Matrix?

Man muss einfach ein Gleichungssystem lösen, dann hat man sie. Toll.

Den Schritt spart die Antwort aus. Deshalb ist die Frage

Daher die Frage, wie berechne ich A^-1

mitnichten beantwortet.

---

Die Frage wie man die Inverse berechnet wurde auf

https://www.mathelounge.de/1070413/gleichungssystem-mit-inverse-lose…

unter anderem auch von mir, beantwortet.

Eigentlich geht es in dieser Frage nur darum, wie man eine Matrix mit einem Vektor multipliziert.

Daher die Frage, wie berechne ich A-1 und B, um auf 3 und 2 zu kommen?

Answer 2

Um die Frage mal vernünftig zu beantworten:

Ein lineares Gleichungssystem lässt sich allgemein schreiben in der Form $Ax=b$. Dabei ist $A$ die sogenannte Koeffizientenmatrix und $b$ die rechte Seite. Durch Multiplikation mit der Inversen von links erhält man $A^{-1}Ax=A^{-1}b$ bzw. $x=A^{-1}b$. Ist die Matrix $A$ also invertierbar, so besitzt das LGS die Lösung $x=A^{-1}b$.

Comments

Die genaue Frage die den Fragesteller umtreibt war:

Daher die Frage, wie berechne ich A-1 und B, um auf 3 und 2 zu kommen?

---

Da die Frage, wie man eine inverse Matrix berechnet, schon an anderer Stelle beantwortet wurde, liegt der Verdacht nahe, dass der Zusammenhang eines LGS mit der Darstellung $Ax=b$ völlig unklar ist und somit auch, was das mit $A^{-1}$ und dem $b$ auf sich hat.