Es erscheint mir hier sinnvoll, zunächst die beiden hinteren Summen auszuwerten.
Dabei ist zu beachten, dass Summen, bei denen der obere Index kleiner als der Startindex ist, üblicherweise als leere Summen mit dem Wert 0 betrachtet werden.
Außerdem ist es ungünstig, dass der dritte Laufindex ebenfalls \(i\) ist, obwohl das hier keine Probleme macht, da nur über 1er summiert wird. Betrachten wir also
\(S_n =\displaystyle \sum \limits_{k=1}^{n}\sum_{i=1}^{k-1}\sum_{{\color{blue}{j=1}}}^{i-1}{1} \)
Schaue nun zuerst, ab wann alle Summen nichtleer sind:
\({\color{orange}{k=1}}\): \(\displaystyle\sum_{i=1}^{\color{orange}{0}}\Rightarrow\) leere Summe = 0
\({\color{orange}{k=2}}\): \(\displaystyle \sum_{i=1}^{1}\sum_{{\color{blue}{j=1}}}^{\color{orange}{i-1}} = \sum_{i=1}^{1}\sum_{{\color{blue}{j=1}}}^{\color{orange}{0}} \Rightarrow\) leere Summe = 0
Ab \(k=3\) sind die Summen damit nichtleer und wir haben für \(\bm{n\geq 3}\):
\(S_n = \displaystyle \sum \limits_{k=1}^{n}\sum_{i=1}^{k-1}\sum_{{j=1}}^{i-1}{1} = \sum_{\color{blue}{k=3}}^{n}\sum_{i=1}^{k-1}\underbrace{\sum_{j=1}^{i-1}{1}}_{= i-1} =\ldots\)
Beachte, dass \(\displaystyle \sum_{j=1}^{i-1}{1}\) nichts anderes ist, als die Summe von \((i-1)\) 1en:
\(\ldots = \sum_{\color{blue}{k=3}}^{n} \underbrace{\sum_{i=1}^{k-1}(i-1)}_{=\frac{(k-2)(k-1)}2} = \ldots \)
Benutze hier, dass \(\displaystyle \sum_{i=1}^{k-1}(i-1)\) die Summe der natürlichen Zahlen von 1 bis \(k-2\) ist. Also zu zeigen ist
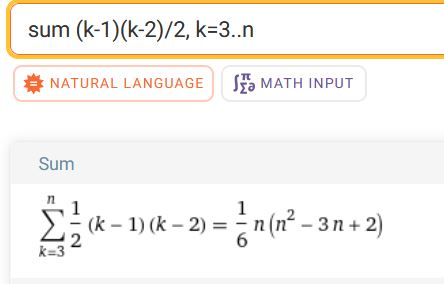
\(\boxed{S_n = \sum_{\color{blue}{k=3}}^{n} \frac{(k-2)(k-1)}2 \text{ für }\bm{n\geq 3}}\)
Das kannst du jetzt per Induktion zeigen.
Dass diese Beziehung tatsächlich gilt, kannst du z. Bsp. so überprüfen: