Finden Sie alle Punkte, in denen die Funktion F lokal invertierbar ist und F^-1 differenzierbar ist.

Question

Aufgabe:

Finden Sie alle Punkte, in denen die Funktion $F$ lokal invertierbar ist und $F^{-1}$
differenzierbar ist !

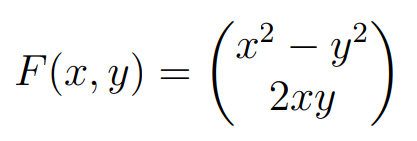
Text erkannt:

$F(x, y)=\left(\begin{array}{c}x^{2}-y^{2} \\ 2 x y\end{array}\right)$

Lösungsansatz:

Mein Ansatz ist folgender: Ich habe mir die Jacobi-Matrix ausgerechnet und weiß, dass wenn die Determinante an einer Stelle ≠0 ist, die Funktion lokal invertierbar ist.

$Df=\begin{pmatrix} 2x & -2y \\ 2y & 2x \end{pmatrix}$

$det(Df)=2x2x-2y*-2y=4x^{2}+4y^{2}$.

Damit die Funktion invertierbar ist muss das ≠0 sein.

Dafür bekomme ich x≠-y

Ist das schon die Lösung? Ist daraus auch $F^{-1}$ differenzierbar?

Danke schon im Voraus!

Comments

Ja, das ist die Lösung. Zum Satz über die lokale Umkehrfunktion gehört auch, dass die Umkehrfunktion differenzierbar ist. Für diese Ableitung gibt es auch eine Formel, die Du mal nachschlagen solltest.

---

Hallo,

vielen Dank für die Hilfe!

Meinst den Satz D(F^-1(x))|_F(x*) =D(F(x))^-1|_x* ?

---

Genau, das meinte ich, allerdings sind auf der rechten Seite die Klammern nicht richtig: [DF(x)]^(-1)

Inverse der Ableitung.