1. Ein Planquadrat hat auf dem Plan mit dem Maßstab 1:200 hat einen Flächeninhalt von 25cm2
wie groß ist der wahre Flöcheninhalt?
Nun, ein Quadrat mit dem Flächeninhalt 25 cm 2 hat eine Seitenlänge von 5 cm.
Bei einem Maßstab von 1 / 200 hat das wahre Quadrat eine um das 200 - fache größere Seitenlänge, also 1000 cm
Und daraus ergibt sich der Flächeninhalt des wahren Quadrates zu
A = 1000 cm * 1000 cm = 1.000.000 cm 2
2.welche Aussage ist falsch:
1.Zwei Dreiecke sind zueinander ähnlich , dann sie in zwei Innenwinkel übereinstimmen
wenn
Die Aussage ist richtig.
Wenn nämlich zwei Innenwinkel bekannt sind, dann ergibt sich der dritte Innenwinkel zu:
Winkel3 = 180 ° - Winkel 1 - Winkel 2
Wenn also zwei Dreiecke in zwei Winkeln übereinstimmen, dann stimmen sie auch in ihrem jeweiligen dritten Winkel überein - und damit sind sie einander ähnlich.
2.in einem Gleichschenkligem Dreieck sind die Basiswinkel gleich groß(ich hab noch nie was von Basiswinkel gehört)
Die Aussage ist richtig.
Ein gleichschenkliges Dreieck besteht aus zwei gleich langen Schenkeln und einer dritten Seite. Diese dritte Seite bezeichnet man als Basis.
Als Basiswinkel bezeichnet man die Winkel an den beiden Enden der Basis.
3.ein Trapez besitzt mind. Ein paar parallele Seiten
Die Aussage ist richtig.
Ein Viereck, dass kein Paar paralleler Seiten besitzt, heißt unregelmäßiges Viereck.
Ein Viereck, das zwei Paare paralleler Seiten besitzt, heißt Parallelogramm.
4ein stumpfwinkliges Dreieck besitzt genau einen stumpfen Winkel(das müsste wahr sein)
Die Aussage ist richtig.
Ein stumpfer Winkel ist ein Winkel der größer als 90 ° ist. Da aber die Innenwinkelsumme eines Dreiecks 180° ist, kann ein Dreieck höchstens einen stumpfen Winkel haben, denn zwei stumpfe Winkel wären alleineschon größer als 180°.
Ein stumpfwinkliges Dreieck muss aber auch mindestens einen stumpfen Winkel haben, da es sonst kein stumpfwinkliges Dreieck wäre.
Daraus folgt, dass ein stumpfwinkliges Dreieck genau einen stumpfen Winkel hat.
5.zwei Dreiecke sind zueinander kongruent zueinander, wenn sie in zwei Seiten und einem Winkel übereinstimmen( müsste auch wahr sein)
Die Aussage ist falsch.
Richtig wäre: "... wenn sie in einem Winkel und den diesem Winkel anliegenden beiden Seiten übereinstimmen."
Dazu ein Gegenbeispiel:
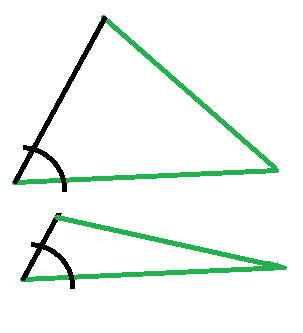
Diese beiden Dreiecke stimmen in den Längen der beiden grün gezeichneten Seiten überein und auch der markierte Winkel ist in beiden Dreiecken gleich groß. Dennoch sind sie offensichtlich nicht kongruent.
ich muss das begründen ob es wahr oder falsch ist:
Die Funktion y=1/x2+1(x ER) besitzt keine Polstelle
Schau genau, welche Funktion gemeint ist:
Die Funktion
f ( x ) = ( 1 / x 2 ) + 1
hat eine Polstelle, nämlich dort, wo der Nenner des Bruches den Wert 0 annnimmt, also bei x = 0
Die Funktion
f ( x ) = 1 / ( x 2 +1 )
hingegen hat keine Polstelle, denn es gibt kein x ∈ R, für welches der Nenner x 2 + 1 den Wert 0 annimmt.
2.Jedes Prisma besitzt sechs Begrenzungsseiten
Die Aussage ist falsch. Ein Prisma hat mindestens 3 Begrenzungsseiten. Es kann aber auch beliebig viele haben.