Wie bringe ich Lineares Problem in Standardform

Question

Folgendes Problem:

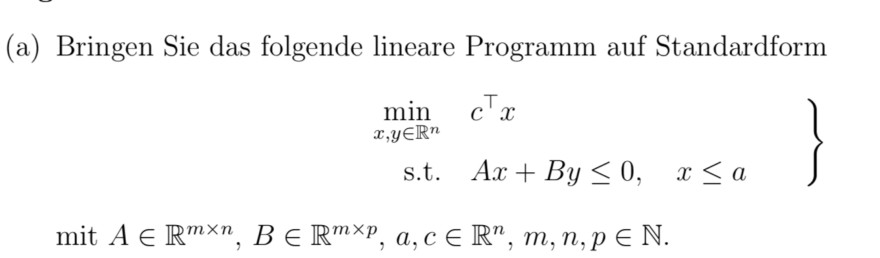
Text erkannt:

(a) Bringen Sie das folgende lineare Programm auf Standardform
$\left.\begin{array}{rl} \min _{x, y \in \mathbb{R}^{n}} c^{\top} x \\ \text { s.t. } & A x+B y \leq 0, \quad x \leq a \end{array}\right\}$

Mein Ansatz wäre nun eine Schlupfvariable s einzuführen, sodass ich Ax+By+s=0 erhalte. Wie kann ich x<=a denn nun so schreiben, dass ich x>=0 erhalte?

Answer 1

Du fügst auch für $x\leq a$ eine Schlupfvariable ein, so dass $x+s_2=a$ mit $s_2\geq 0$. Für unbeschränkte Variablen nutzt man den Ansatz $x=x^+-x^-$ mit $x^+,\ x^-\geq 0$.

Comments

Okay, danke.

Jetzt ist aber die Defintion der Standardform ja eigentlich, dass x>=0 sein soll. Wie stelle ich das denn dar? Habe ich dann drei Nebenbedingungen (einmal die Bedingungen mit den zwei schlupfvariablen und  >=0) oder hab ich nur zwei Nebenbedingungen?

---

Du ersetzt $x$ durch die Variabeln $x^+$ und $x^-$, mit $x^+,\ x^-\geq 0$.

Mit $x^+-x^-=x$ hast du dann die Nebenbedingung als Gleichung, aber die Variablen $x^+$ und $x^-$ erfüllen die Nichtnegativitätsbedingung.

---

Also wäre meine Lösung dann

Min c^Tx

s.t. Ax=-By-s₁

x+s₂ = a

Mit x=x⁺-x^-  wobei x⁺ und x^->0