f(x)= x²-3x+2
f ( x ) = x^2 - 3 * x + 2
a) Schränke den Defintionsbereich ein
Eine natürliche Einschränkung für den Definitionsbereich gibt
es nicht. Man kann den Definitionsbereich ( willkürlich ) ein-
schränken z.B. auf D = [1..4]
b) Bilde die Umkehrfunktion
y = x^2 - 3 * x + 2
Umkehrfunktion ( y und x tauschen )
x = y^2 - 3 * y + 2 | nach y umstellen
y^2 - 3 * y + 1.5^2 = x - 2 + 1.5^2 | quadratische Ergänzung
( y - 1.5 )^2 = x + 0.25 | Wurzel ziehen
y - 1.5 = ±√ ( x + 0.25 )
y = ± √( x + 0.25 ) + 1.5
Es gibt 2 Umkehrfunktion
y = √( x + 0.25 ) + 1.5
y = - √( x + 0.25 ) + 1.5
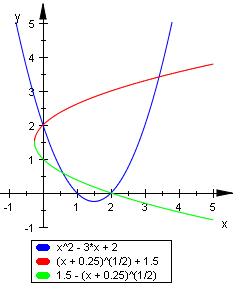
Blau ist f. Rot und grün die Umkehrfunktionen.
Der Def Bereich für die Umkehrfunktion ist eingeschränkt
da die Wurzel nur aus einem Wert >= Null gezogen werden kann.
Also x + 0.25 >= 0. x >= -0.25
D = [ -0.25 ; ∞ [
Bei Fehlern oder Fragen wieder melden.
mfg Georg
c) Zeichnen Sie beide Funktionen