Wahrscheinlichkeiten Ermitteln, mithilfe von Histogrammen

Question

Aufgabe

Text erkannt:

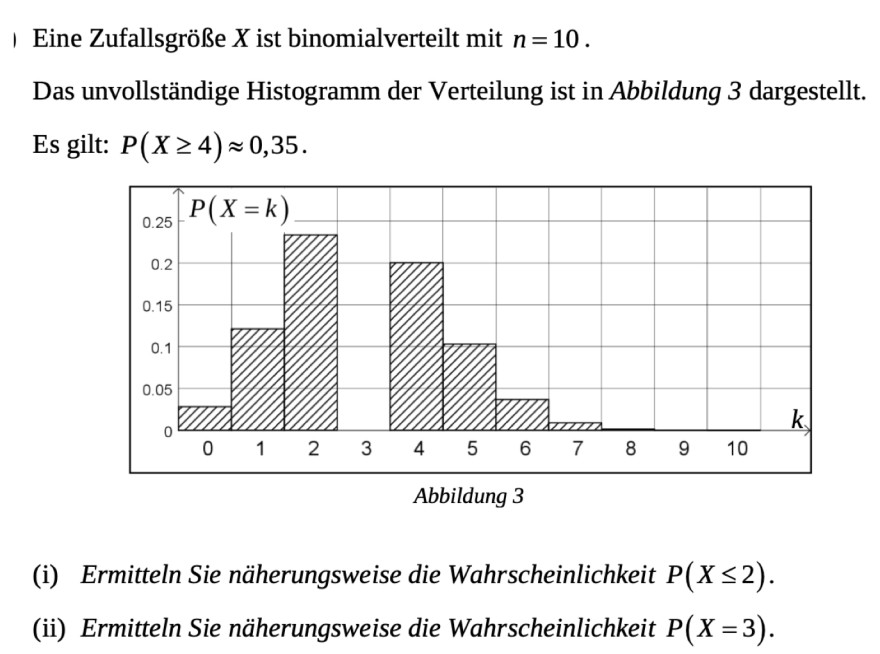
Eine Zufallsgröße $X$ ist binomialverteilt mit $n=10$.
Das unvollständige Histogramm der Verteilung ist in Abbildung 3 dargestellt. Es gilt: $P(X \geq 4) \approx 0,35$.

Abbildung 3
(i) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P(X \leq 2)$.
(ii) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P(X=3)$.

Kann mir jemand helfen diese Aufgabe zu lösen? Hab alles ausprobiert, komme aber auf das falsche Ergebnis :(

Comments

Hab alles ausprobiert, komme aber auf das falsche Ergebnis :(

Mit dieser Aussage kann man nicht viel anfangen. Was hast Du ausprobiert, was waren Deine Ergebnisse?

---

Hab alles ausprobiert

Wirklich alles ?

- den ungefähren Verlauf des Histogramms schätzen und erkennen, dass das Maximum der Verteilung bei k=3 liegen wird
- wissen, wie Lehrer ticken und annehmen, dass p=3/10 (weil ein einfacher Wert) ist
- ausprobieren, was dann P(k=4) sein wird (Ergebnis : 0,2001)
- hinreichend gute Übereinstimmung mit dem Histogramm feststellen und den Rest berechnen.

---

Ich lese jeweils ungefähr ab:

P(0) = 0,03

P(1) = 0,12

P(2) = 0,24

P(4) = 0,205

P(5) = 0,105

P(6) = 0,04

P(7) = 0,01

-> P(3) = 1- 0,35- 0,39 = 0,26

Answer 1

(i) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P(X \leq 2)$.

Die Höhen der entsprechenden Balken addieren.

(ii) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P(X=3)$.

$P(X\leq 2) + P(X=3) + P(X\geq 4) = 1$ weil auf jeden Fall genau eines der drei Ereignisse eintritt.