Aufgabe:
Kann jemand meinen Fehler bitte finden?
Das Ergebnis der Reihe müsste 3,033 sein, und ich habe 3,283 raus

Text erkannt:
e). (a) Berechnen Sie den Wert der Reihe:
\( \sum \limits_{k=2}^{\infty}\left(\frac{7 \cdot(-2)^{k+2}}{5^{k}}-3^{-k}\right) \)
nzwerte der Folgen:
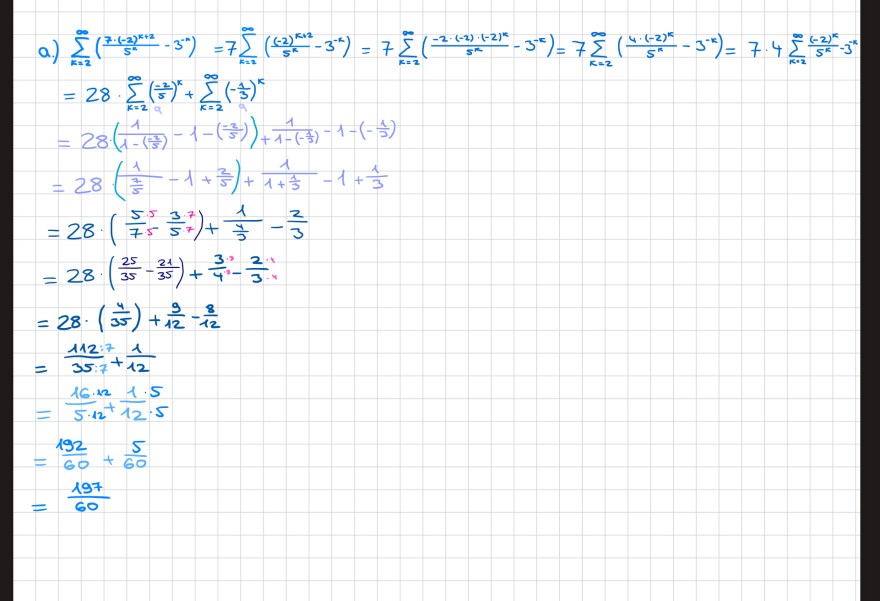
Text erkannt:
a.) \( \begin{aligned} & \sum \limits_{k=2}^{\infty}\left(\frac{7 \cdot(-2)^{k+2}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{(-2)^{k=1}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{-2 \cdot(-2)^{(-2)^{k}}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{4 \cdot(-2)^{k}}{5^{k}}-3^{-k}\right)=7 \cdot 4 \sum \limits_{k=2}^{\infty} \frac{(-2)^{k}}{5^{k}}-3^{-k} \\ = & 28 \cdot \sum \limits_{k=2}^{\infty}\left(\frac{-2}{5}\right)^{k}+\sum \limits_{k=2}^{\infty}\left(-\frac{1}{3}\right)^{k} \\ = & 28 \cdot\left(\frac{1}{1-\left(\frac{-2}{5}\right)}-1-\left(\frac{-2}{5}\right)\right)+\frac{1}{1-\left(-\frac{1}{3}\right)}-1-\left(-\frac{1}{3}\right) \\ = & 28 \cdot\left(\frac{1}{\frac{7}{5}}-1+\frac{2}{5}\right)+\frac{1}{1+\frac{1}{3}}-1+\frac{1}{3} \\ = & 28 \cdot\left(\frac{5 \cdot 5}{7 \cdot}-\frac{3 \cdot 7}{5} 7\right)+\frac{1}{\frac{4}{3}}-\frac{2}{3} \\ = & 28 \cdot\left(\frac{25}{35}-\frac{21}{35}\right)+\frac{3 \cdot 3}{4}-\frac{2}{3} \cdot 4 \\ = & 28 \cdot\left(\frac{4}{35}\right)+\frac{9}{12}-\frac{8}{12} \\ = & \frac{112: 7}{35: 7}+\frac{1}{12} \\ = & \frac{16 \cdot 12}{5 \cdot 12}+\frac{1 \cdot 5}{12 \cdot 5} \\ = & \frac{192}{60}+\frac{5}{60} \\ = & \frac{197}{60}\end{aligned} \)
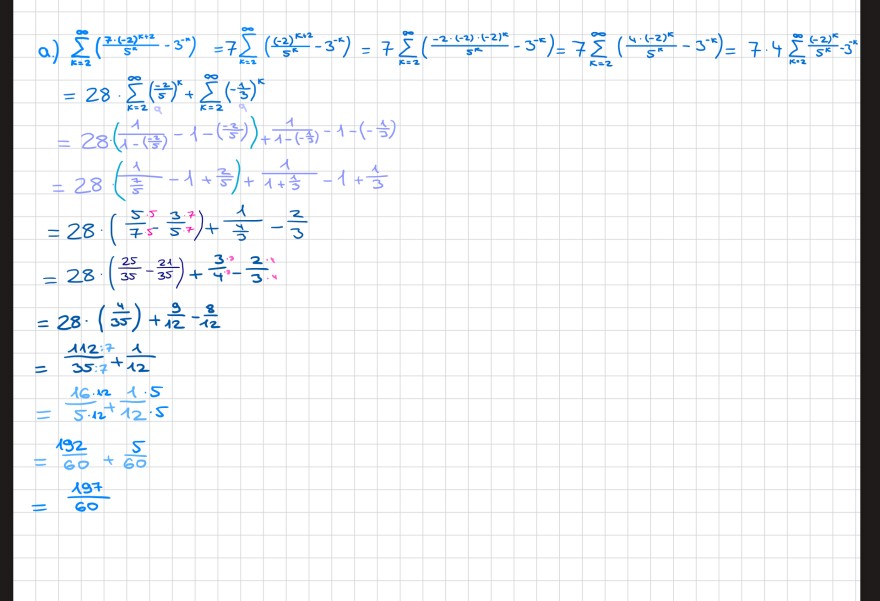
Text erkannt:
a.) \( \begin{aligned} & \sum \limits_{k=2}^{\infty}\left(\frac{7 \cdot(-2)^{k+2}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{(-2)^{k=1}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{-2 \cdot(-2)^{(-2)^{k}}}{5^{k}}-3^{-k}\right)=7 \sum \limits_{k=2}^{\infty}\left(\frac{4 \cdot(-2)^{k}}{5^{k}}-3^{-k}\right)=7 \cdot 4 \sum \limits_{k=2}^{\infty} \frac{(-2)^{k}}{5^{k}}-3^{-k} \\ = & 28 \cdot \sum \limits_{k=2}^{\infty}\left(\frac{-2}{5}\right)^{k}+\sum \limits_{k=2}^{\infty}\left(-\frac{1}{3}\right)^{k} \\ = & 28 \cdot\left(\frac{1}{1-\left(\frac{-2}{5}\right)}-1-\left(\frac{-2}{5}\right)\right)+\frac{1}{1-\left(-\frac{1}{3}\right)}-1-\left(-\frac{1}{3}\right) \\ = & 28 \cdot\left(\frac{1}{\frac{7}{5}}-1+\frac{2}{5}\right)+\frac{1}{1+\frac{1}{3}}-1+\frac{1}{3} \\ = & 28 \cdot\left(\frac{5 \cdot 5}{7 \cdot}-\frac{3 \cdot 7}{5} 7\right)+\frac{1}{\frac{4}{3}}-\frac{2}{3} \\ = & 28 \cdot\left(\frac{25}{35}-\frac{21}{35}\right)+\frac{3 \cdot 3}{4}-\frac{2}{3} \cdot 4 \\ = & 28 \cdot\left(\frac{4}{35}\right)+\frac{9}{12}-\frac{8}{12} \\ = & \frac{112: 7}{35: 7}+\frac{1}{12} \\ = & \frac{16 \cdot 12}{5 \cdot 12}+\frac{1 \cdot 5}{12 \cdot 5} \\ = & \frac{192}{60}+\frac{5}{60} \\ = & \frac{197}{60}\end{aligned} \)