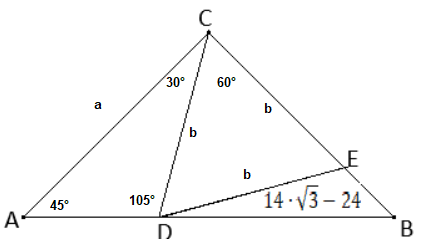
Wir können b durch a mit dem Sinussatz ausdrücken:
b= a·\( \frac{sin 45°}{sin105°} \).
Nun gilt sin 105° = sin 75° = sin (45°+30°) = sin 45° · cos 30° + cos 45° · sin 30°
= \( \frac{\sqrt{2}}{2} \) · \( \frac{\sqrt{3}}{2} \) +\( \frac{\sqrt{2}}{2} \) ·\( \frac{1}{2} \)
= \( \frac{\sqrt{2}}{2} \) · (\( \frac{\sqrt{3}}{2} \) +\( \frac{1}{2} \))
Damit gilt
b= a·\( \frac{sin 45°}{sin105°} \) = a·\( \frac{1}{\frac{\sqrt{3}}{2} + \frac{1}{2}} \).
Der Flächeninhalt des Dreiecks ABC ist a²/2.
Der Flächeninhalt des Dreiecks ADC ist 0,5ab·sin30°= \( \frac{1}{4(\frac{\sqrt{3}}{2} + \frac{1}{2})}a^2 \).
Der Flächeninhalt des Dreiecks DEC ist \( \frac{\sqrt{3}}{4}b^2=\frac{\sqrt{3}}{4}( \frac{1}{\frac{\sqrt{3}}{2} + \frac{1}{2}})^2a^2\).
Der Inhalt des Dreiecks DBE lässt sich dann durch
a²/2 - \( \frac{1}{4(\frac{\sqrt{3}}{2} + \frac{1}{2})}a^2 \)-\(\frac{\sqrt{3}}{4}( \frac{1}{\frac{\sqrt{3}}{2} + \frac{1}{2}})^2a^2\) ausdrücken.
Setzt man diesen Term gleich 14\( \sqrt{3} \)-24, erhält man a.
Kürzer ist vermutlich der Ansatz
\(14 \sqrt{3}-24 \) = 0,5 · b (a-b) · sin 120° mit a= b·(\( \frac{\sqrt{3}}{2} + \frac{1}{2}\) ).
Daraus wird
\(14 \sqrt{3}-24 \) = 0,5 · b (\( \frac{\sqrt{3}}{2} - \frac{1}{2}\))b ·\(\frac{\sqrt{3}}{2}\)
\(14 \sqrt{3}-24 \) = \( \frac{b^2}{8} \cdot(3-\sqrt{3})\)
\(b^2=\frac{8\cdot(14 \sqrt{3}-24)}{3-\sqrt{3}}=\frac{8\cdot(14 \sqrt{3}-24)(3+\sqrt{3})}{6}=\frac{8\cdot(-30+18\sqrt{3})}{6}=8\cdot (3\sqrt{3}-5)\)
Mit Koordinatengeometrie:
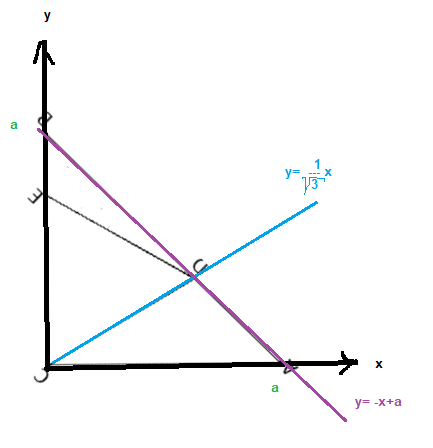
Schnittpunkt D der beiden linearen Funktionen berechnen, Abstand CD als y-Koordinate von E verwenden,
BE ist Grundseite, und x-Koordinate von D ist Höhe des Dreiecks BED.