h: x →-x-1 ; x ≤-2 und p: x → 1,5 x+2, x ≥ 0 mit …

Question

Text erkannt:

1. a) Zeigen Sie, dass Sie die beiden Straßenstücke aus Beispiel 2.2 \( h: x \rightarrow-x-1 ; x \leq-2 \) und \( p: x \rightarrow 1,5 x+2, x \geq 0 \) mit einer ganzrationalen Funktion r dritten Grades durch Interpolation verbinden können.
b) Stellen Sie die drei abschnittweise definierten Funktionen graphisch dar.
c) Begründen Sie, warum die Interpolation durch eine ganzrationale Funktion dritten Grades möglich ist, während die Interpolation durch eine Funktion zweiten Grades nicht möglich ist.

Aufgabe:

Problem/Ansatz:

Text erkannt:

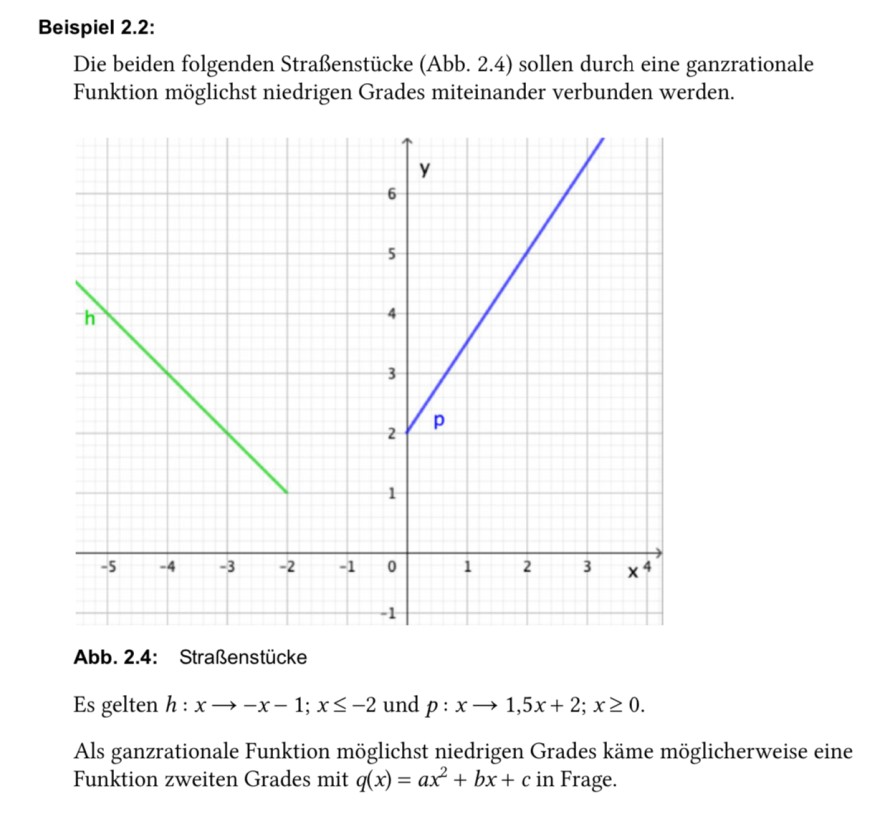
Beispiel 2.2:
Die beiden folgenden Straßenstücke (Abb. 2.4) sollen durch eine ganzrationale Funktion möglichst niedrigen Grades miteinander verbunden werden.

Abb. 2.4: Straßenstücke
Es gelten \( h: x \rightarrow-x-1 ; x \leq-2 \) und \( p: x \rightarrow 1,5 x+2 ; x \geq 0 \).
Als ganzrationale Funktion möglichst niedrigen Grades käme möglicherweise eine Funktion zweiten Grades mit \( q(x)=a x^{2}+b x+c \) in Frage.

Bin ganz neu hier und bräuchte hier Hilfe in Mathe, so ganz genau weiß ich auch nicht wie das ganze funktioniert, ich hoffe das ist verständlich gezeigt worden. Bin für jeden Tipp und Hilfe dankbar

Answer 1

An den Anschlussstellen müssen die Funktionswerte und die Steigungen übereinstimmen (stetig und knickfrei). Daraus lassen sich Gleichungen aufstellen (wie viele?). Das führt auf ein LGS, welches eindeutig lösbar ist. Man könnte auch noch fordern, dass die zweiten Ableitungen an den Stellen übereinstimmen (ruckfrei).