Du hast mit dem Satz
Ich muss ja als erstes das Baumdiagramm machen
des Pudels Kern getroffen. Mach also als erstes das Baumdiagramm.
Wenn es dann nicht weitergeht, lade es hier hoch und berichte wo der Schuh drückt, und jemand wird weiterhelfen.
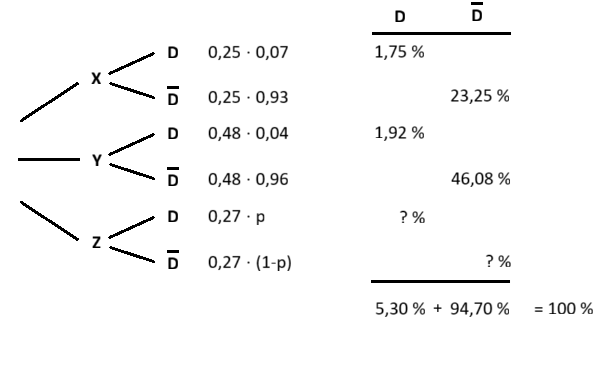
Für a) sollte man noch die beiden Fragezeichen durch Werte ersetzen.
Bei b) komme ich auf \( p = 1,63 / 27 \approx 6 \, \% \)
und bei c) auf \( p = 1,92 / 5,3 \approx 36 \, \% \)