Eigenmann: Gesucht wird die Länge der Hypotenuse

Question

Aufgabe:

Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.4.167, ISBN 3-12-722310-2, 1981, S. 24.

Problem/Ansatz:

Vorsicht: Maße sind keine Radien

Comments

Eigenmann hat auch Lösungen mitgeliefert. Zu dieser Aufgabe schrieb er:

[spoiler]

\(\displaystyle 17 \, \text{cm} \)

[/spoiler]

(eingangs zitiertes Werk, S. 57)

Answer 1

Nur Pythagoras:

15^2 + (x - 9)^2 = x^2 → x = 17

Comments

Natürlich. Alles andere ist overkill.

Answer 2

Hallo,

ich unterstelle, dass die Punkte auf der Horizontalen die Mittelpunkte der beiden Kreise sein sollen. Dann liefert die Konstruktion mit Zirkel und Lineal ...

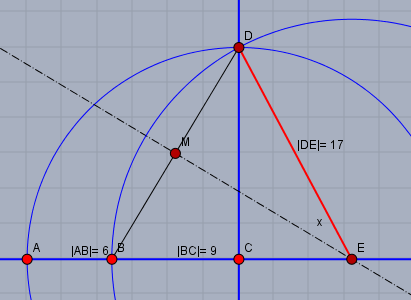
... \(x=17\). Das rechtwinklige Dreieck \(\triangle EDC\) hat demnach die Seitenlängen \(15,\, 8,\, 17\), welche ein pythagoreisches Tripel bilden.

Comments

mit Höhensatz des Euklid:

h² = p • q  >>  15² = 9 • q >>  q = 25  >>  p + q = 2x   >>  x = (9 + 25) / 2 = 17

Werner-Salomon:

demnach die Seitenlängen (15, 8, 17)

Die Seite mit Länge  8 ist doch erst nach dem Ergebnis (Seite der Länge 17)
gemäß Rechnung von mathecoach bekannt.

---

Inwiefern liefert die Konstruktion denn \(x=17\)? Es könnte doch auch \(x=16,999995\) oder \(y=17,0012345\) sein. Also nachmessen wird man das sicherlich nicht (können).

---

Die Seite mit Länge 8 ist doch erst nach dem Ergebnis (Seite der Länge 17)

Das stimmt nicht. Mittelsenkrechte von der Strecke BD ergibt:

y = - 9/15·(Ex + 9/2) + 15/2 = 0 → Ex = 8