Gegeben ist die Funktion f(x) mit:

Die Punkte P ( 0 | f(0 ) , Q ( 0 | u ) und R ( u | f(u) ) bilden für u > 0 ein Dreieck. Berechnen Sie, für welchen Wert von u der Inhalt des Dreiecks maximal wird.
Mein Ansatz ist bisher diese Skizze:
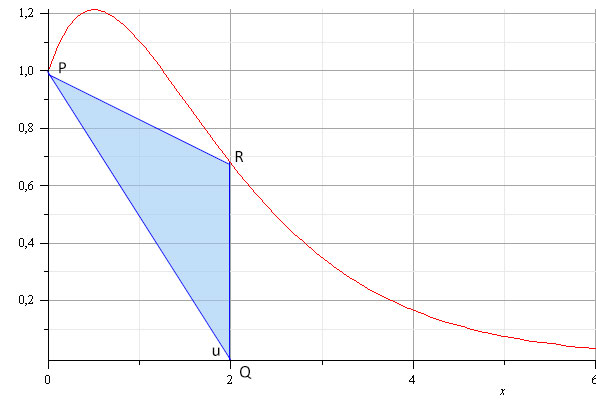
Es gibt zwar auch eine Lösung zu der Aufgabe, diese ist aber sehr minimalistisch, sodass ich daraus nicht schlau werde..
Die Nebenfunktion ist ja klar, das ist die Funktionsgleichung f(x)..
Aber wie komme ich an die Funktion für den Flächeninhalt des Dreiecks, also die Zielfunktion?
MfG
Thomagedu