Mal zu Aufgabe b)
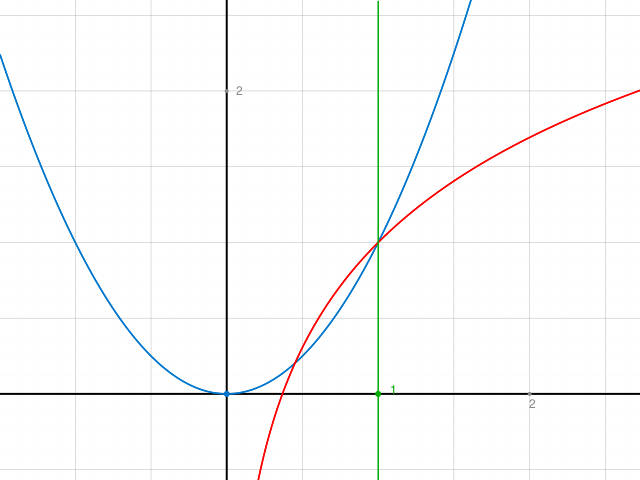
Die Nahtstelle ist bei x=1.
Der Graph von f(x) besteht links von x=1 aus der blauen und rechts davon aus der roten Kurve.
Im Punkt P(1/1) schneiden sich die beiden Graphen, denn 1^2 = 1 und ln (1) + 1 = 0 + 1 = 1
Deshalb ist die Funktion in der Nahtstelle stetig.
Sie ist dort aber nicht differenzierbar. Das siehst du daran, dass in P(1/1) zwischen der blauen und der roten Kurve ein Winkel ≠ 0 liegt. Also ein Knick vorliegt.
Um das rechnerisch zu zeigen, musst du die beiden Teilfunktionen ableiten und 1 einsetzen. Dann siehst du, dass die Steigungen von links (blaue Kurve) und rechts (rote Kurve) nicht übereinstimmen.
(ln(x) + 1)' = 1/x x=1 einsetzen: Steigung 1.
(x^2)' = 2x x=1 einsetzen: Steigung 2.
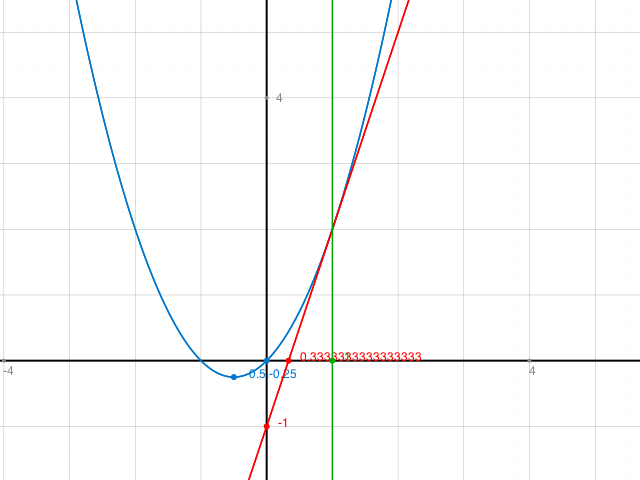
Bei Aufgabe a) machst du genau dasselbe.
f(x) : links der Naht die rote Kurve (Gerade) und rechts davon die blaue Kurve.
x =1 einsetzen in x^2 +x → 1^2 + 1 =2
x=1 einsetzen in 3x-1 → 3-1 = 2
Somit stetig in x=1.
(x^2 +x)' = 2x + 1 -----> x=1 einsetzen: Steigung in 1 ist 3
(3x-1)' =3 Konstant. Steigung in 1 ist 3
Daher f(x) differenzierbar in x=1.