Zeichne die Vektoren, aber wie soll ich das zeichen?

Question

$$ a)   \left(\begin{matrix} 2\\5\\3 \end{matrix}\right)
b) \left(\begin{matrix} -3\\2\\4 \end{matrix}\right)
c) \left(\begin{matrix} -2\\4\\-3 \end{matrix}\right) $$

wie zeichnet man diese Vekoren in ein 3 Dimensionales Koordinatensystem oder kann man die auch in ein normales Koordinatensystem einzeichen?

Und bei a) ist noch so ein Pfeil über a, und bei b) auch über b und bei c) auch über c

Answer 1

In ein "normales" (also zweidimensionales) Koordinatensystem kann man nur Vektoren mit höchstens zwei Dimensionen einzeichnen. Für die vorliegenden dreidimensionalen Vektoren ist ein dreidimensionales Koordinatensystem erforderlich.

Der Vektor a sieht in einem solchen etwa so aus:

 

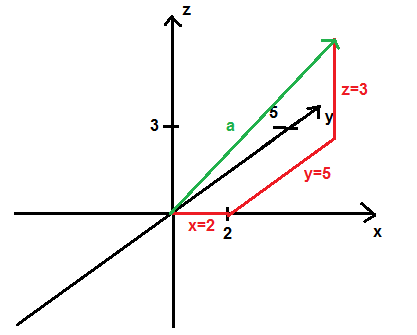
Und bei a) ist noch so ein Pfeil über a, und bei b) auch über b und bei c) auch über c

Der Pfeil über dem a, dem b und dem c kennzeichnet diese als Vektoren.

Und vermutlich steht hinter dem a, dem b und dem c auch keine schließende Klammer sondern ein Gleichheitszeichen, richtig?

Comments

Ahso ok Danke für den Hinweis :)

Das heißt also

2 5 3 das heißt 2 ist mein x und dann gehe ich 5 bei y und dann 3 bei z?

---

So ist es :-)

---

Wow cool Danke :)

würdest Du mir auch bei meiner anderen Frage helfen bitte :)