ich bitte euch, meine Lösungen zu überprüfen.Sorry, dass ich meine Lösungen als Links hochlade. Bin nämlich neu hier und schaffe es schon nicht, mich mit den Formeln auseinanderzusetzen.
1) Betrachten Sie die geometrische Reihe, die beschrieben wird durch a0 =-4 und den Faktor q = (1+x). Geben Sie an, für welche x-Werte die unendliche Summe bestimmt werden kann und bestimmen Sie die unendliche Summe für diese Fälle (Formel und Ergebnis inAbhängigkeit von x).
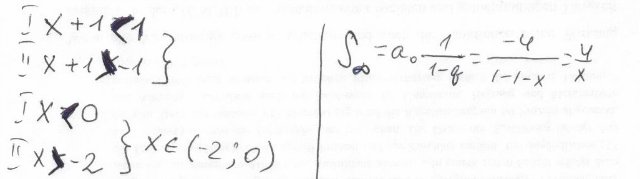
2) Sie wollen über einen Sparplan Geld anlegen, um in 40 Jahren bei Renteneintritt Geld zur Verfügung zu haben. Der Zinssatz von 4% wird dabei zugrunde gelegt und jeweils am Jahresende gezahlt.
1. Sie zahlen anfangs 5000 Euro ein und anschließend über 40 Jahre jeweils zu Jahresende 1200 Euro. Geben Sie an, wie hoch Ihr Vermögen jeweils am Ende von Jahr n ist (als Formel) und wie hoch das Vermögen nach 40 Jahren (nach der letzten Einzahlung) ist (Wert angeben).
3.Bestimmen Sie den zu 4% konformen Monatszins
4. Wie hoch muss bei 5000 Euro Anfangszahlung die monatliche Einzahlung (erste Einzahlung im Folgemonat und monatliche Zinsabrechnung) in 40 Jahren insgesamt 200000 Euro zusammenkommen.

3) Eine Investition in Höhe von R0 = -84 480 ergibt den beiden Folgejahren Einnahmen in Höhevon R1 = 40 000 und R2 = 50 000.
1. Bestimmen Sie den Kapitalwert bei dem Kalkulationszinssatz von 5%.
2. Geben Sie die Gleichung an, die Sie lösen müssen um den internen Zinsfuß zu bestimmen.
3. Berechnen Sie den internen Zinsfuß .4. Führen Sie die ersten beiden Schritte eines Intervallhalbierungverfahrens (Bisektion) durch,wobei Sie mit rA = 0 und rB = 0; 05 starten und geben Sie an, ob Sie nach zwei Schritten enden, wenn die Genauigkeit c = 1000 ist.

4)Betrachten Sie die Funktion f(x) = (3/4)(1-x^2) für -1 < (oder gleich) x <(oder gleich) 1 und f(x) = 0 sonst.
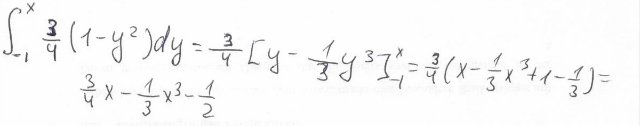
Danke schon mal