Kurvendiskussion von Exponentialfunktion: f(x) = (x-1)2*e-x/2

Question

(x-1)^2*e^{-x/2} die erste und zweite Ableitung

 

1) Wendepunkte

2) können sie mir auch die Extremstellen  zeigen.

Hoch- und Tiefpunkt und am Schluss den Graph

3) limes x----> unendlich

Answer 1

Du musst hier die Produktregel verwenden und bei den Ableitungen der Faktoren die Kettenregel beachten:

f(x) = (x-1)²*e^-x/2

u = (x-1)²         u' = 2*(x-1)

v = e^-x/2        v' = -0.5 * e^-x/2

f ' (x) = 2(x-1)* e^-x/2  + (x-1)² * (-0.5)*e^-x/2         |e^ausklammern

      = (2x - 2 + (-0.5)* (x² - 2x + 1)) * e^-x/2

      = (2x - 2 - 0.5x² + x - 0.5) * e^-x/2

 f '(x)     = - (0.5x² - 3x + 2.5)*e^-x/2              |fertig!

Andere Schreibweise:  (-0.5) ausklammern und faktorisieren.

  = -0.5 * (x² - 6x + 5)*e^-x/2

  = -0.5*(x-1)(x-5)*e^-x/2

 

Die zweite Ableitung kannst du gleich machen.

f '(x)     = - (0.5x² - 3x + 2.5)*e^-x/2

u = - (0.5x² - 3x + 2.5)            u' = - (x - 3) = - x + 3

v, v' wie oben

f ''(x)  = (-x+3)* e^-x/2   - (0.5x² - 3x + 2.5) * (-0.5)*e^-x/2         |e^ausklammern

      =( (-x+3) - (0.5x² - 3x + 2.5)*(-0.5)) *e^-x/2

      = (3-x + 0.25x² -1.5 x + 1.25) * e^-x/2

f ''(x)     = (0.25x² - 2.5x + 4.25)*e^-x/2              |fertig!

 

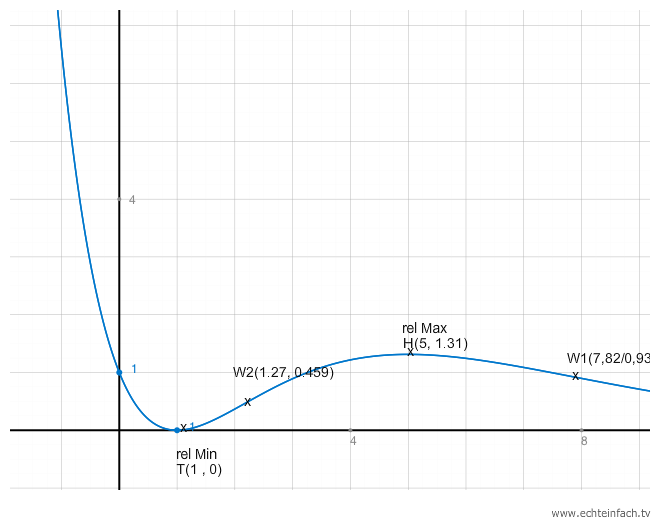
Wenn du die Wendepunkte brauchst, musst du diese Ableitung 0 setzen. Dabei kann nur das Polynom Null werden

Also statt

 (0.25x² - 2.5x + 4.25)*e^-x/2    =0

nur (0.25x² - 2.5x + 4.25)   = 0        |: 0.25

x² - 10x + 17 = 0

pq Formel

x1,2 = 5 ± 2√2   in den Taschenrechner eingeben. f(x1) und f(x2) ausrechnen.

 

2) Für die Extremalstellen  die erste Ableitung 0 setzen. Dafür ist die 2. Form der ersten Ableitung ideal

 

Andere Schreibweise:  (-0.5) ausklammern und faktorisieren.

0  = -0.5 * (x² - 6x + 5)*e^-x/2

0  = -0.5*(x-1)(x-5)*e^-x/2

x1 = 1, x2 = 5

Beide x-Werte in f(x) einsetzen: Der höhere Wert ist das lokale Maximum der andere das lokale Minimum.

f(1) = 0 lokales Minimum und f(5) = etwas über 1 genauer noch ausrechnen: lokales Maximum. Kontrolle: Graph

 

3) limes x -> ± unendlich (x-1)²*e^-x/2

Die Exponentialfunktion ist immer stärker als eine Polynomfunktion. Das vorhandene Polynom ist immer ≥ 0.

Daher  

limes x -> unendlich (x-1)²*e^-x/2 

 

=  limes x -> unendlich e^-x/2 = 0

(von oben gegen x-Achse)

 

 limes x -> - unendlich (x-1)²*e^-x/2 

 

=  limes x -> - unendlich e^-x/2 = + unendlich.

 

 

Alles noch nachrechnen!

 

 

 

Comments

1)      bei der 2. ableitung  haben sie                 2) können sie mir auch die Extremstellen  zeigen

= (3-x + 0.25x^2 -1.5 x + 1.25) * e^{-x/2}                 Hoch und Tiefpunkt und am schluss den Grapf

f ''(x)     = (0.25x^2 + 2.5x - 4.25)*e^{-x/2}                3) limis x geht durch unendlich

aber bei mir ist es so rausgekommen                         

= (3-x + 0.25x^2 -1.5 x + 1.25) * e^{-x/2}                             viellllllllllleeen Dankkk!

f"(x) = e^{-x/2}*(4,25-2,5x+0,25x^2)

            weil       3-1,25 = 4,25 und

                         -x-1,5x = kommt -2,5x raus oder...

                          und 0,25x^2 bleibt normal

---

Danke für den Hinweis. Ich hab jetzt die Vorzeichen korrigiert.

---

=  limes x -> unendlich e^{-x/2} = 0

(von oben gegen x-Achse

also ich hab das so ausgerechnet

lim x-> unendlich (x-1)^2*e(-x/2)= (unendlich - 1)^2*e(-unendlich/2)= (unendlich)^2*e(-unendlich/2)

                                                                                                                        = unendlich*e(-unendlich/2)

                                                                                                                        = 1/ e(unendlich/2)

                                                                                                                    = kommt da jetzt null raus

                                                                                                                       und wenn ja warum

da hab ich jetzt ergebnisse von hoch ,tiefpunkt und wendestellen können sie es bitte kontrollieren danke

1) H(5/1,31)     2) T(1/0)

1)W1(7,82/0,932)     2) W2(2,17/0,459) wenns passt können sie es mir den Grapf zeichnen

soooorryyyyy dass ich zu viele Fragen stelle

---

Deine Resultate sind eingezeichnet. Sieht gut aus.

 

Mit dem Grenzwert kannst du folgendermassen überlegen (schreiben solltest du das aber nicht unbedingt. Gleich das Resultat sieht mathematischer aus):

unendlich / 2 = unendlich.

e^unendlich = unendlich

1/ e(unendlich/2) = 1/e^unendlich = 1/unendlich → 0

Zähler immer 1. Der Bruch wird beliebig klein, wenn der Nenner beliebig gross wird.

---

hab noch eine Frage

Auf der Grapf (y-Achse)

wie kommen sie auf (1/0) diesen Strich nach oben

und die letzten zwei Fragen

Monotonie und Krümmung

also bei mir ist es so

Monotonie:                                                             Krümmung:

]-unendlich,1[ streng monoton fallend          ]-unendlich,2,17[ positiv/ linksgekr

]1,5[ streng monoton steigend                       ]2,17,7,8[ negativ/ rechtsgekr.

]5,unendlich[ streng monoton fallend           ]7,8,unendlich[ negativ / rechtsgekr.

---

soooooorrrrryyy ich meine (0 und 1)

---

"Auf der Graph (y-Achse)

wie kommen sie auf (1/0) diesen Strich nach oben" 

Du meinst wohl (0,1) den y-Achsenschnittpunkt.

Hier muss man in der Funktionsgleichung x=0 einsetzen.

f(0) = 1 * e⁰ = 1*1 = 1

"und die letzten zwei Fragen

Monotonie und Krümmung

also bei mir ist es so

Monotonie:                                                             Krümmung:

]-unendlich,1[ streng monoton fallend          ]-unendlich,2,17[ positiv/ linksgekr

]1,5[ streng monoton steigend                       ]2,17,7,8[ negativ/ rechtsgekr.

]5,unendlich[ streng monoton fallend           [7,8,unendlich[ negativ / rechtsgekr."

ist beides ok 

Ich habe bei der Krümmung noch die Stelle 7.8 ergänzt (rote Klammer). Grund: Ableitung an dieser Stelle auch negativ.

---

Hier muss man in der Funktionsgleichung x=0 einsetzen.

f(0) = 1 * e^0 = 1*1 = 1

warum muss ich da 0 einsetzen muss ich das immer machen

muss ich bei jedem Beispiel 0 in die ursprungliche Funktion einsetzen

oder ist es nur bei dem Beispiel

---

Das kannst du mit jeder Funktion so machen. Lies mal https://de.wikipedia.org/wiki/Kurvendiskussion genau durch.

---

da haben sie geschrieben Zaehler immer 1. der bruch wird beliebig klein,wenn der nenner beliebig gross wird das verstehe ich nicht so ganz koennen sie mir einen beispiel geben danke

---

Beispiel:

1/10 = 0.1

1/100 = 0.01

1/1000 = 0.001

usw. Grenzwert (Zähler 1 und Nenner gegen unendlich) ist 0.

---

ok also das heisst bei lim x geht durch unendlich kommt immer 0 raus wenn nicht was kann noch alles rauskommen