Kurvendiskussion: f(x) = x^3 - 3x^2 - x + 3. Gleichung der Wendetangente?

Question

Hallo ihr klugen köpfe ,ich hoffe mir kann jemand detailliert erklären wie man vorgeht:

Gegeben sei die Funktion f : x → x^3 - 3x^2 - x + 3

a) Untersuchen Sie die Funktion auf Symmetrie zum Ursprung bzw. zur y-Achse.

b) Die Funktion ist punktsymmetrisch zum Punkt P(1|0). Beweisen Sie dies, indem Sie zeigen, dass die Identität f(1-x) = -f(1+x) für alle x ∈ ℝ gilt.

c) Bestimmen Sie die Nullstellen der Funktion sowie den Schnittpunkt mit der y-Achse.

d) Bestimmen sie die Ableitungsfunktionen f', f'' und f'''.

e) Untersuchen Sie die Funktion auf Hoch- und Tiefpunkte.

f) Bestimmen Sie den Wendepunkt der Funktion.

g) Zeichnen Sie den Graph der Funktion für -1,5 < x < 3,5. Orientieren Sie sich dabei an den Resultaten aus a) - f). Berechnen Sie erforderlichenfalls einige zusätzliche Funktionswerte.

h) Bestimmen Sie die Steigung der Funktion in den Achsenschnittpunkten. Berechnen Sie den jeweiligen Schnittwinkel.

i) Welche Steigung liegt im Wendepunkt vor? Bestimmen Sie die Gleichung der Wendetangente.

j) Weisen Sie nach, dass dreimal der Funktionswert 1 angenommen wird. Berechnen Sie ein x ∈ ℝ mit f(x) = 1 näherungsweise auf zwei Kommastellen genau.

 

Answer 1

f(x) = x^3 - 3x^2 - x + 3

a)

Keine Symmetrie zur y Achse und zum Ursprung, da sowohl gerade als auch ungerade Potenzen von a auftreten.

b)

f(1-x) = -f(1+x)
(1-x)^3 - 3(1-x)^2 - (1-x) + 3 = -((1+x)^3 - 3(1+x)^2 - (1+x) + 3)
(-x^3 + 3x^2 - 3x + 1) - 3(x^2 - 2·x + 1) - (1-x) + 3 = -((x^3 + 3x^2 + 3x + 1) - 3(x^2 + 2·x + 1) - (1+x) + 3)
4x - x^3 = 4x - x^3

Damit ist die Symmetrie gezeigt.

c)

Y-Achsenabschnitt f(0) = 3

Nullstellen f(x) = 0

x³ - 3x² - x + 3 = 0

Über eine Wertetabelle findet man die Nullstellen -1, 1 und 3. Da es keine weiteren Nullstellen geben kann brauche ich keine Polynomdivision machen.

d)

f(x) = x³ - 3x² - x + 3
f '(x) = 3x^2 - 6x - 1
f ''(x) = 6x - 6
f '''(x) = 6

e) 

Extrempunkt f '(x) = 0
3x^2 - 6x - 1 = 0

Die abc-Formel liefert die Stellen
x1 = 1 + 2/3*√3 = 2.155
x2 = 1 - 2/3*√3 = -0.155

f(1 + 2/3*√3) = -16/9·√3 = -3.079
f(1 - 2/3*√3) = 16/9·√3 = 3.079

HP(-0.155 | 3.079)
TP(2.155 | -3.079)

f)

Wendepunkt f ''(x) = 0
6x - 6 = 0
x = 1

f(1) = 0

WP(0 | 1)

g)

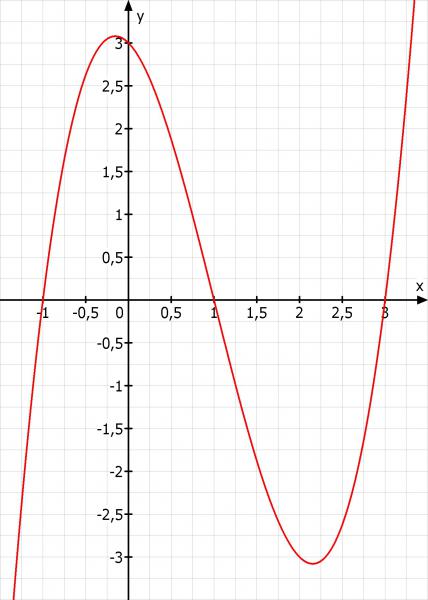
h)

f '(0) = -1 → Winkel von 45 Grad mit der Y-Achse
f '(-1) = 8 → Winkel von arctan(8) = 82.87 Grad
f '(1) = -4 → Winkel von arctan(-4) = -75.96 Grad
f '(3) = 8 --> Winkel von arctan(8) = 82.87 Grad

i)

f '(1) = -4

t(x) = -4 * (x - 1) = -4x + 4

j)

Der HP befindet sich über 1 und der TP unter 1. Damit geht der Graph 3 mal durch die Gerade mit der Gleichung y = 1.

f(x) = 1
x^3 - 3x^2 - x + 3 = 1
x^3 - 3x^2 - x + 2 = 0

x_n+1 = x_n - (x_n^3 - 3x_n^2 - x_n + 2)/(3x_n^2 - 6x_n - 1)

Erste Näherung für die ganz rechte Nullstelle ist x1 = 3

x2 = 3.125
x3 = 3.115
x4 = 3.115

Damit habe ich das jetzt sogar auf 3 Nachkommastellen gerechnet.