Wie Nachkommastellen von Pi selbst berechnen?

Question

Gibt es zum Berechnen der Nachkommastellen von Pi einen Algorithmus, wenn ja, welchen?

Wie berechnen die Computer das? Vielleicht kann mir das jemand einfach erklären.

!

Answer 1

Hier ist eine PDF aus dem Netz: Ausgewählte Algorithmen zur Berechnung von Pi (0,7 MB) Quelle hier

Es handelt sich übrigens bei den "Berechnungen" stets um Annäherungen, da Pi unendlich viele Ziffern nach dem Komma hat.

In der Lektion Bogenmaß und Kreiszahl Pi zeigen wir, wie sich die Kreiszahl Pi berechnen/annähern lässt, und zwar mit Hilfe von Polygonen und Sinus:

Je mehr Polygon-Seiten wir wählen, desto genauer wird der Wert für Pi.

Probiere das Programm einfach selbst aus: PI - Annäherung über Umfang. Es gibt noch ein zweites Programm mit Berechnung, siehe PI - Annäherung über Fläche

Answer 2

Schau mal hier: http://www.pi-zahl.de/

LG

Answer 3

$$ \sum _ { n = 1 } ^ { \infty } \frac { 1 } { n ^ { 2 } } = \frac { 1 } { 1 ^ { 2 } } + \frac { 1 } { 2 ^ { 2 } } + \frac { 1 } { 3 ^ { 2 } } + \frac { 1 } { 4 ^ { 2 } } + \cdots = \frac { \pi ^ { 2 } } { 6 } $$

Leichte Formel... oder?

Answer 4

Versuch es mit dieser Formel:

$$ \pi = \tan 1 \times 10 ^ { - n } \times 180 \times 1 \times 10 ^ { n } $$

Faktoren:

$$ 180 = \tan 1 \times 10 ^ { - n } \times 180 \times 1 \times 10 ^ { \mathrm { n } } / \tan 1 \times 10 ^ { - 1 } / 1 \times 10 ^ { \mathrm { n } } \\ \tan = \tan 1 \times 10 ^ { - 1 } \times 180 / 180 \\ \tan ^ { - 1 } \left( \tan 1 \times 10 ^ { - n } \times 180 / 180 \right) = 1 \times 10 ^ { - 1 } $$

Beispiel:

$$ \pi = \tan 1 \times 10 ^ { - 48 } \times 180 \times 1 \times 10 ^ { 48 } = 3.141592653589793238462643383279502884197169375105820974 ... $$

Alternative: Berechnung mit dieser Exhaustion Methode

$$ \pi = \tan 1 \times 10 ^ { - 1 } \times \mathrm { r } ^ { 2 } / 2 \times 360 \times 10 \mathrm { n } / \mathrm { r } ^ { 2 } $$

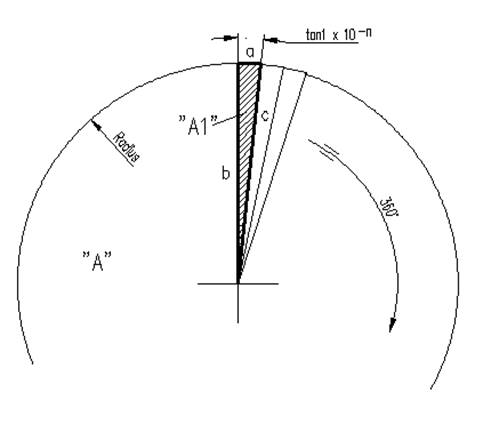
Faktoren:

$$ A 1 = \tan 1 \times 10 ^ { - n } \times r ^ { 2 } / 2 \\ A = \tan 1 \times 10 ^ { - n } \times r ^ { 2 } / 2 \times 360 \times 10 ^ { n } $$

Beispiel:

$$ r = 17,3 \\ \tan = 1 \times 10 ^ { - 48 } \\ \pi = \tan 1 \times 10 ^ { - 48 } \times 17.32 / 2 \times 360 \times 10 ^ { 48 } / 17.3 ^ { 2 } = 3.1415926535897932384626495028841971693993751074944 ... $$