Funktionenschar untersuchen zur Funktionsgleichung: fa(x)= x*ln(a * x)

Question

Bitte um hilfe, habe das thema verpasst

Untersuche dir Funktionenschar f_a(x)= x*ln(a * x) unter folgenden Gesichtspunkten:

1) Definitionsbereich

2) verhalten von fa an den Rändern des Definitionsbereiches,

3) schnitpunkte mit der x-Achse

4) relative Extrempunkte

5) wendepunkte

=> a>0

 

Answer 1

f_a(x)= x * ln(a * x) mit a > 0

1) Definitionsbereich 

Der ln ist nur für positive Zahlen definiert. Damit muss x ∈ ℝ⁺ sein.

2) verhalten von fa an den Rändern des Definitionsbereiches, 

lim _x→∞ fa(x) = ∞

lim _x→0 fa(x) = x * ln(a *x) = ln(a * x) / (1/x) = (1/x) / (- 1/x^2) = -x = 0

3) schnitpunkte mit der x-Achse 

x * ln(a * x) = 0

x kann nicht Null werden damit muss folgendes gelten:

ln(a * x) = 0
a * x = 1
x = 1/a

4) relative Extrempunkte 

fa'(x) = 0
ln(a·x) + 1 = 0
x = 1/(e*a)

5) wendepunkte

fa''(x) = 0
1/x = 0

Das ist nie erfüllt, also gibt es keinen Wendepunkt.

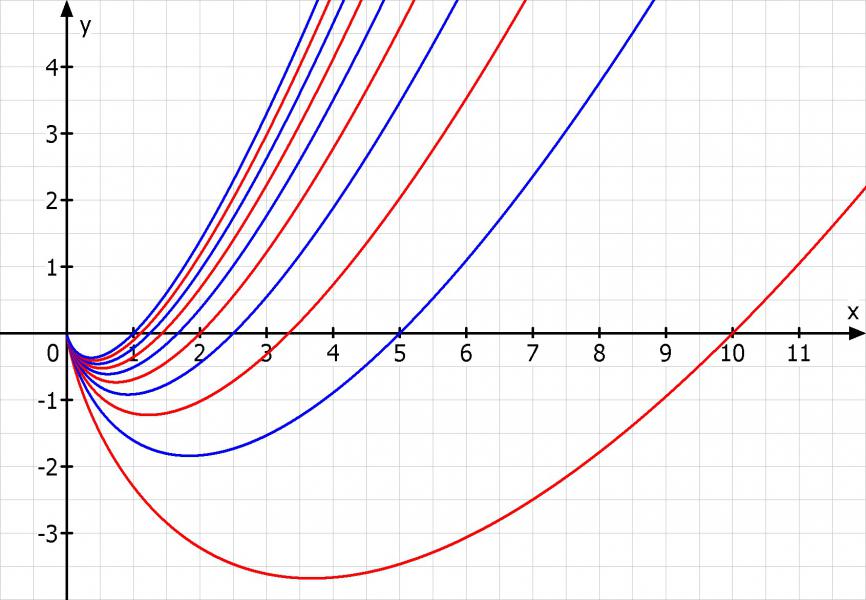
Skizze: