Berechne die Wahrscheinlichkeit, dass zwei verschiedenfarbige Kugeln gezogen werden, wenn mit Zurücklegen gezogen wird

Question

   In einer Urne befinden sich 8 rote und 6    blaue Kugeln.    Es wird zweimal je eine Kugel gezogen. a)  Berechne die Wahrscheinlichkeit, dass zwei verschiedenfarbige Kugeln gezogen   werden, wenn mit zurück legen gezogen wird

Kann mir jemand sagen wie ich das löse?

Answer 1

Hi :)

 In einer Urne befinden sich 8 rote und 6 blaue Kugeln.

Es entsteht also folgender Baum:

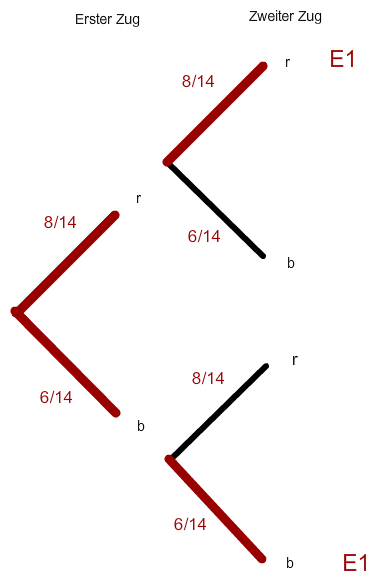
So, nun einfach die Pfadregeln anwenden:

$$ P({ E }_{ 1 }) = \frac { 4 }{ 7 }\cdot\frac { 4 }{ 7 } + \frac { 3 }{ 7 }\cdot\frac { 3 }{ 7 } = \frac { 16 }{ 49 } + \frac { 9 }{ 49 } = \frac { 25}{ 49 } ≈ 0,51 $$

Das entspricht etwa 51%.

Bei Fragen melde dich, ich hoffe, es hat etwas geholfen.

Comments

Hm...

"... verschiedenfarbige..."?

---

Ups, dann halt genau die anderen beiden Pfade...sorry das tut mir sehr leid :((

---

und wie sieht das ann aus? der rechenweg?

---

$$ P({ E }_{ 1 }) = \frac { 4 }{ 7 }\cdot\frac { 3 }{ 7 } + \frac { 3 }{ 7 }\cdot\frac { 4 }{ 7 } = \frac { 12 }{ 49 } + \frac { 12 }{ 49 } = \frac { 24 }{ 49 } ≈ 0,49 $$

Man hätte gar nicht rechnen müssen. Oben habe ich dir die Gegenwahrscheinlichkeit des Ereignisses berechnet, denn wenn du nicht zwei verschiedenfarbige Kugeln ziehst, ziehst du logischerweise zwei farbige. Dieses Prinzip kann man sich bei komplexeren Aufgaben (also bei Aufgaben, wo man die Bäue nicht mehr zeichnen kann) zu Nutze machen. Das musst du dann von 1 subtrahieren und kommst auf etwa 0,49. Das sind dann 49%.

---

vielen dank schonmal für die Antworten! wie würde das ganze aussehen wenn ohne zurücklegen gezogen wird?

---

So hier: