Wieviele Schüler lernen eine bzw. zwei Sprachen?

Question

In einer Klasse sind 40 Schüler. Jeder lernt mindestens eine der Sprachen Deutsch, Englisch und Französisch. 34 Schüler lernen  mindestens  eine der beiden Sprachen Deutsch und Englisch. 25 Schüler lernen  mindestens  eine Sprache Deutsch und Französisch. 6 Schüler lernen nur Deutsch. Genau zwei Sprachen Deutsch und Englisch lernen drei Schüler mehr als Französisch und Deutsch. Kein Schüler lernt Englisch und  Französisch.

Wie viele Schüler lernen genau eine bzw. genau zwei Sprachen?

Wer kann mir helfen. Wie kann ich die Formel aufstellen?

Comments

Wer sagt, dass du eine Formel aufstellen musst?

Am einfachsten dürfte die Aufgabe werden, wenn du ein Mengendiagramm (Venndiagramm) zeichnest. 

Answer 1

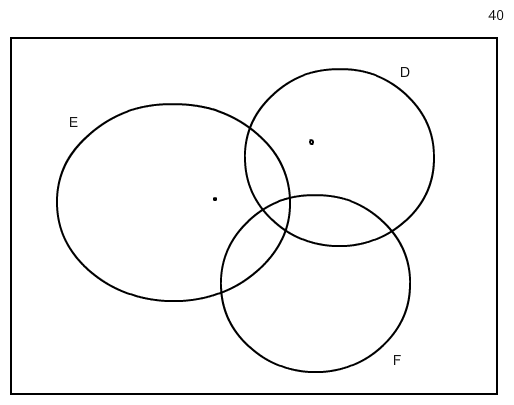
Die 40 stehen im 1. Satz.

Im 2. Satz steht: alle lernen mindestens eine dieser Sprachen. Daher ist nun im Restfeld aussen eine 0.

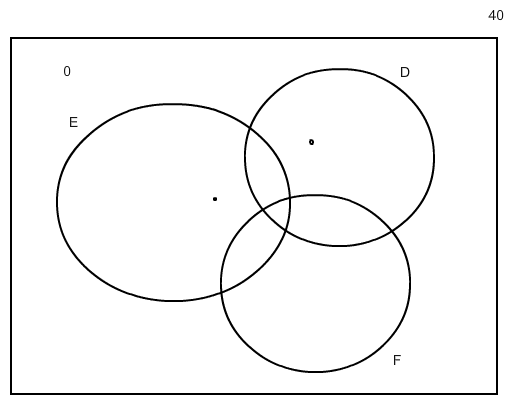
Nun suchst du weitere Sätze im Text, die dir erlauben eines der Felder zu füllen. Ich sehe da 6, die nur Deutsch lernen und keinen, der E und F lernt. Wenn der letzte Satz logisch richtig formuliert ist, kommen neben der schwarzen auch die blaue Null aus diesem Satz.

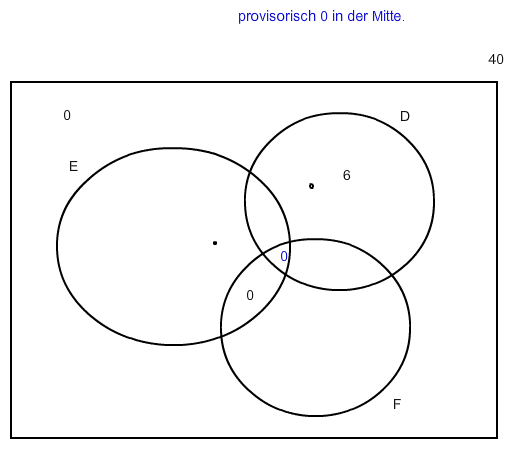
Nun hast du noch 4 Felder offen und 40 - 6 = 34 Kinder zu verteilen. Lies die andern Sätze ganz genau und fülle die leeren Felder noch. 

Comments

Danke, aber bringt mich der Lösung leider nicht näher. Bin so schlau wie vorher 

---

Jetzt kann man für x die Zahlen 1,2,3,4,5,6 einsetzen und so die 4 Felder noch füllen. 

Ich sehe keine Möglichkeit aus dem Text, die Lösungsmöglichkeiten weiter einzuschränken. Aber lies selbst nochmals genau.