Funktionsgleichung erstellen 3 Grades mit dem Hochpunkt (0|7.2] Nullstellen [0|-2] , [0|3]

Question

Ich muss die Funktionsgleichung erstellen und mir sind gegeben

Hochpunkt : [0|7.2]
Nullstellen : [-2|0]

Nullstellen : [3|0]

Und ich muss a,b, c und d herausfinden. 

Wie rechne ich das mit der Gleichung f(x)= ax²+bx+cx+d

Answer 1

Für eine Funktion 3. Grades hast du :

f(x)= ax^3+bx^2+cx+d

Jetzt hast du noch f'(x)= 3ax+2bx+c

Jetzt hast du gegeben :
 f(-2) = 0

f(3) = 0

f(0) = 7,2

Und

f'(0) = 0

Daraus kannst du ein Lineares Gleichungssystem erstellen und dies dann auflösen .

Answer 2

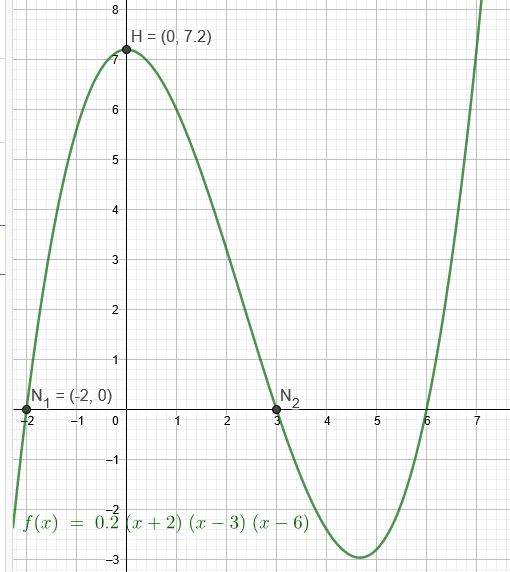
Hochpunkt : \((0|7,2)\)
Nullstellen :  \((-2|0)\) oder \((3|0)\)

\(f(x)=a(x+2)(x-3)(x-N)\)

\(f(0)=a(0+2)(0-3)(0-N)=6aN\)

\(6aN=7,2\)

\(a=\frac{7,2}{6N}=\frac{1,2}{N}\)

\(f(x)=\frac{1,2}{N}[(x^2-x-6)(x-N)]\)

\(f´(x)=\frac{1,2}{N}[(2x-1)(x-N)+(x^2-x-6)]\)

\(f´(0)=\frac{1,2}{N}[(-1)(-N)+(-6)]\)

\(\frac{1,2}{N}[N-6]=0\)

\(N=6\)    \(a=\frac{1,2}{6}=0,2\)

\(f(x)=0,2(x+2)(x-3)(x-6)\)