Bestimmen Sie die Ableitungen (e-Funktionen und deren Unterschiede)

Question

Aufgabe 12 - Ableitungen von e-Funktionen:

a) Ordnen Sie die Funktionsgraphen den Funktionsgleichungen zu.

\( f_{1}(x)=2 e^{x} \)

\( f_{2}(x)=e^{2} \)

\( f_{3}(x)=e^{x-2} \)

\( f_{4}(x)=0,5 e^{x}-3 \)

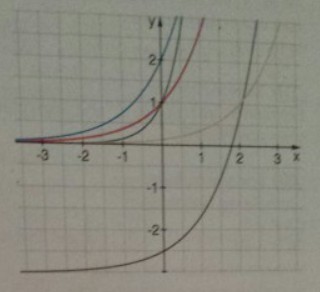
Durch welche geometrischen Abbildungen gehen diese jeweils aus dem Graphen von \( f(x)=e^{x} \) hervor?

b) Bestimmen Sie die Ableitungen und zeichnen Sie deren Graphen.

c) Wie unterscheiden sich die Ableitungsgraphen von dem Graphen der Ableitung von \( f(x)=e^{x} \) ?

Aufgabe 13 - Ableitungen:

Erläutern Sie, wie man den Graphen von \( f(x)=e^{x} \), „bewegen“ muss, um die Graphen der angegebenen Funktionen zu erzeugen. Geben Sie zudem die zugehörige Ableitung an.

a) \( f(x) = -e^{x}+5 \)

b) \( f(x)=0,1 \cdot e^{x+6} \)

c) \( f(x)=\left(\frac{1}{e}\right)^{x}-e \)

d) \( f(x)=-e^{-x} \)

Comments

Wie man vom Graphen von f(x) zum Graphen von f'(x) kommt:

Bei 13a) muss der Graph von f(x) um -5 in y-Richtung verschoben werden.

Bei 12.4. muss der Graph von f(x) um +3 in y-Richtung verschoben werden.

Bei 12.1. und 13.b) stimmen der Graph von f(x) und f ' (x) überein.

Mehr, wenn alle Ableitungen vorhanden sind.

---

Ableitung von f1(x)=2*e^x Von f2(x)= -2e^x f3(x) = e^{x-2} Ableitung von 0.5e^x +3 = 0.5e^x

---

https://www.matheretter.de/tools/funktionsplotter/

e^{2x + ln(2)}   blau

2e^{2x}           rot

e^2x    lila

2e^{2x - ln(2)} grün

Da blau und rot, sowie lila und grün zusammenfallen, siehst du, dass man da auch Verschiebungen parallel zur x-Achse drinn hat.

Jetzt könntest du ja deine Ableitungen im Plotter eingeben und den Exponenten etwas abändern.

Answer 1

ich mach mal ein Beispiel aus der Nummer 13.

$$0,1*{ e }^{ x+6 }$$

Um den Graph dieser Funktion aus dem Graph der Funktion $${e}^{x}$$ zu erhalten, musst du den Graphen in y-Richtung mit dem Faktor 0,1 stauchen und den Graph um 6 Einheiten auf der x-Achse nach links verschieben.

So ähnlich funktioniert das auch mit den anderen 3 Aufgaben ;)

Gruß
EmNero

Comments

Zu 2. Die Funktion $$f(x)={e}^{x+6}$$ liefert für x=-6 den selben Wert wie $$g(x)={e}^{x}$$ für den Wert x=0. -6 liegt links von 0, deswegen ist der Graph nach links verschoben worden.

Allgemein kann man sagen, daas wenn man zu x etwas addiert der Graph nach links und wenn man von x etwas subtrahiert der Graph nach rechts verschoben wird.

Gruß
EmNero

---

12b) Die Ableitungsfunktionen bestimmen.

12c) Untersuchen, wie diese durch Verschiebung aus der Ableitungsfunktion von $${e}^{x}$$ hervorgehen

---

Sorry meinte nicht 12 und c sondern die Aufgabe a den unteren Teil " welche Geometrische Abbildungen.."

---

Das bedeutet wie du den Graph e^x verschieben/strecken/stauchen musst, um diese Graphen zu erhalten.

---

Wo liegt den der zusammenhang zwischen der Verschiebung und der Geometeischen Abbildung

---

Naja verschieben, spiegeln, strecken, stauchen sind sozusagen geometrische Abbildungen ^^

Answer 2

a) f(x) = -e^x + 5 aus g(x) = e^x erzeugen:

1. g spiegeln an der x-Achse -----> h mit h(x) = -e^x

2. h(x) um +5 Einheiten parallel zur y-Achse verschieben → f

3. Da f ' (x) = h(x) , hat man nach 1. bereits f ' (x).

b)

f(x) = 0.1 * e^{x+6}

1. Möglichkeit (analog zu dem, was du bei der Scheitelpunktform von Parabelgleichungen gelernt hattest)

1. g(x) um -6 parallel zur x-Achse verschieben.

2. Mit dem Faktor 0.1 in y-Richtung stauchen.  ------> f(x). Hier zufällig gerade auch f '(x).

2. Möglichkeit. Umformung. 0.1 = e^ ( ln (0.1))

f(x) = e^ (ln(0.1)) * e^{x+6} = e^ ( x + 6 + ln(0.1))

Somit einfach g(x) um -6 - ln(0.1) in x-Richtung verschieben.

Analog bei den andern Aufgaben.

Comments

Auch wenn es dreist erscheint, könntest du mir die anderen beiden Aufgaben auch noch machen?, oder zumindest eine ähnliche Aifhane mit der Erklärung was in der Aufgabe übehautp genau verlangt wird. ln hatten wir noch nicht.

---

Lies hier https://www.matheretter.de/wiki/quadratische-funktionen

Zusammenfassung des Wissens über quadratische Funktionen. https://www.matheretter.de/wiki/quadratische-funktionen

Da wird erklärt, was Stauchung und Verschiebung ist. So schön ist das in einer Antwort hier nicht möglich. Du kannst alles auf Exponentialfunktionen übertragen.

f(x) = - e^{-x}

1. g(x) = e^x Spiegeln an der y-Achse. → h(x) = e^{-x}

2. h(x) spiegeln an der x-Achse → f(x) = - e^{-x}

3. Weil f ' (x) = -(-e^{-x}) = e^{-x}, hast du bei 1. bereits f ' (x).

---

Wie gehe ich den bei Aufgaben wie bei 13.C vor?

Also Aufgaben mit dem Faktor (1/e)^x davor?

---

f(x) = (1/e)^x + e    | Potenzgesetze

= e^{-x} + e

1. g(x) = e^x an der y-Achse spiegeln. --> h(x) = e^{-x}

2. h(x) um e = 2.7... in y-Richtung verschieben ---> f(x) = e^{-x} + e

f ' (x) = -e^{-x}

1. wie oben.

2. h(x) an der x-Achse spiegeln.