Rekonstruktion von der ganzrationalen Funktion dritten Grades mit Extrema in O(0/0) und P(2/4)

Question

Der Graph einer ganzrationalen Funktion dritten Grades hat im Ursprung und im Punkt P(2/4) jeweils ein Extremum.

Answer 1

Hi,

f(x)=ax³+bx²+cx+d

f'(x)=3ax²+2bx+c

 

 

Mit

f(0)=0

f'(0)=0

f(2)=4

f'(2)=0

 

Gleichungen die sich daraus ergeben:

d = 0
c = 0
8a + 4b + 2c + d = 4
12a + 4b + c = 0

(Also:

8a+4b=4

12a+4b=0)

 

a=-1

b=3

 

-> f(x) = -x³ + 3x²

 

Grüße

 

Comments

Ich versteh nicht so ganz wie du a und b ausgerechnet hast ... kannst du mir das nochmal erklären, bitte ?

---

8a+4b=4

12a+4b=0

Damit bist Du einverstanden?

Löse nach 4b auf und setze gleich:

4-8a=-12a  |+12a-4

4a=-4

a=-1

 

Damit in II: -12+4b=0 -> b=3

 

Alles klar? ;)

---

Oh man ich bin so blöd haha :D danke nochmaaaaal !

---

Kein Ding ;).

---

Hey ich verstehe nicht ganz warum  da 12a+4b+c raus kommen 

Ich setze doch in f'(x) = 3ax² +2bx+c ein

Also f'(2)= 3a*4²+2b*4+c

Wäre doch dann 48a+8b +c 

Oder wo liegt mein Fehler?

---

Du setzt doch 2 ein. Nicht 4 :).

Grüße

Answer 2

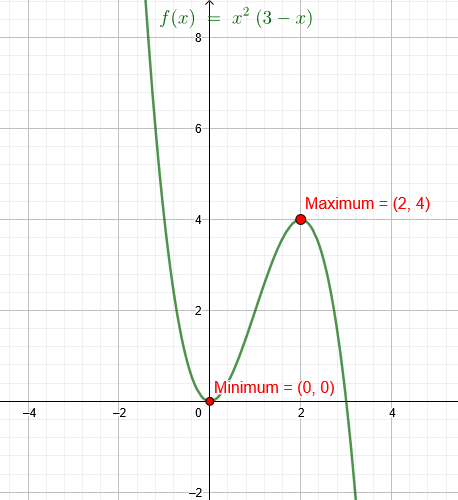
"Der Graph einer ganzrationalen Funktion dritten Grades hat im Ursprung und im Punkt P(2|4) jeweils ein Extremum."

$f(x)=a*x^2*(x-N)$

$f(2)=a*2^2*(2-N)=4a*(2-N)$

$4a*(2-N)=4→a=\frac{1}{2-N}$

$f(x)=\frac{1}{2-N}*[x^2*(x-N)]$

$f´(x)=\frac{1}{2-N}*[2x*(x-N)+x^2]$

$f´(2)=\frac{1}{2-N}*[2*2*(2-N)+2^2]$

$\frac{1}{2-N}*[4*(2-N)+4]=0→N=3$         $a=\frac{1}{2-3}=-1$

$f(x)=(-1)*x^2*(x-3)=x^2*(3-x)$