Ermitteln Sie die Ableitung der Funktion f(x) = -x². Wie funktioniert Ableiten?

742 Aufrufe

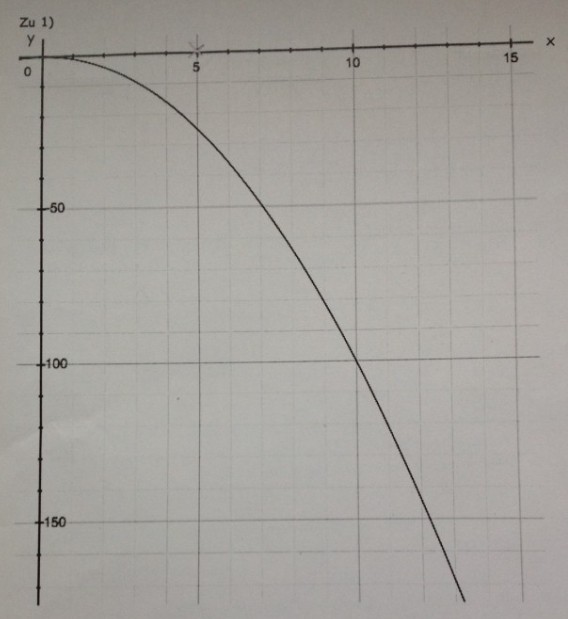
Aufgabe 1: Zeichnen Sie an den Graphen der Funktion $f$ die Tangente in den Punkten P $(5 /-25)$ und $Q(10 /-100)$ . Bestimmen Sie anschließend die Steigung von $f$ in diesen beiden Punkten.

Aufgabe 2: Ermitteln Sie die Ableitung der Funktion $f(x)=-x^{2}$ an verschiedenen Stellen $x_{0}$ mit Hilfe des GTR. Tragen Sie ihre Ergebnisse in die Wertetabelle ein.

$x_{0}$	0	1	2	3	4	5	6	7	8	9	10
$f^{\prime}\left(x_{0}\right)$

Aufgabe 3: Vergleichen Sie die Steigungen, die sie zeichnerisch bestimmt haben (Aufgabe 1), mit denen, die Sie mit dem GTR bestimmt haben (Aufgabe 2). Erklären Sie, wie die Unterschiede zustande kommen.

Aufgabe 4: Stellen Sie die Werte aus der Wertetabelle in einem Koordinatensystem dar.

Aufgabe 5: Beschreiben Sie die Ableitung von $\mathrm{f}$ mit Hilfe einer Funktionsgleichung.
Die Ableitung der Funktion $f(x)=-x^{2}$ an der Stelle $x_{0}$ beträgt $f^{\prime}\left(x_{0}\right)=$