Betrachten Sie die folgenden sechs Funktionen fi: ℕ0 → ℕ0, i = {1, ..., 6}.

Question

Wir verstehen unter $f(n)$ immer $max\left\{ 0,⌈f(n)⌉ \right\}$.

${ f }_{ 1 }(n)={ n }^{ 2 }$    ${ f }_{ 2 }(n)={ n }^{ 3 }$    ${ f }_{ 3 }(n)={ n }^{ 2 }log(n)$  

${ f }_{ 4 }(n)={ 2 }^{ n }$    ${ f }_{ 5 }(n)=log(n)$     ${ f }_{ 6 }(n)={ 2n }^{ 2 }+3n+4$

Füllen Sie folgende Tabelle aus, indem Sie für jedes Paar $({ f }_{ i },{ f }_{ j })$ entweder $Ο,Ω$ oder $Θ$ eintragen. Tragen Sie $Θ$ ein, genau dann wenn ${ f }_{ i }∈ Θ({ f }_{ j })$ gilt. Ansonsten tragen Sie $Ο$ bzw. $Ω$ ein, wenn ${ f }_{ i }∈ Ο({ f }_{ j })$ bzw. ${ f }_{ i }∈ Ω({ f }_{ j })$ gilt.

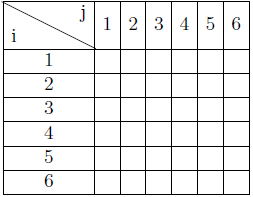
Könnte jemand helfen?

Comments

- o o o n -

n - n o n n

n o - o n n

n n n - n n

o o o o - o

- o o o n -

- = Θ

o = Ο

n = Ω

:)

---

Vielen vielen Dank. ;)