Gegeben seien die komplexen 2x2-Matrizen. Berechnen Sie: A·B, B·A und A+B

Question

hi leute, muss die aufgaben abgeben und krieg's nicht alleine hin sie zu lösen. kann mir vielleicht einer helfen?

(a) Gegeben seien die komplexen \( 2 \times 2 \) - Matrizen
$$ A=\left(\begin{array}{cc} {1+2 i} & {3-i} \\ {5} & {2+i} \end{array}\right), B=\left(\begin{array}{cc} {-2+i} & {4+2 i} \\ {-1} & {-7-3 i} \end{array}\right) \in M(2, \mathrm{C}) $$
Berechnen Sie \( A \cdot B, B \cdot A \) und \( A+B \)

(b) Finden sie alle komplexen Zahlen \( z \) mit \( z^{2}=-24-70 i \)

(c) Zeigen Sie, dass die komplexen Zahlen
$$ z_{0}=1, \quad z_{1}=-\frac{1}{2}+\frac{\sqrt{3}}{2} i, \quad z_{2}=-\frac{1}{2}-\frac{\sqrt{3}}{2} i $$
die Gleichung \( z^{3}=1 \) erfüllen.

Answer 1

a)

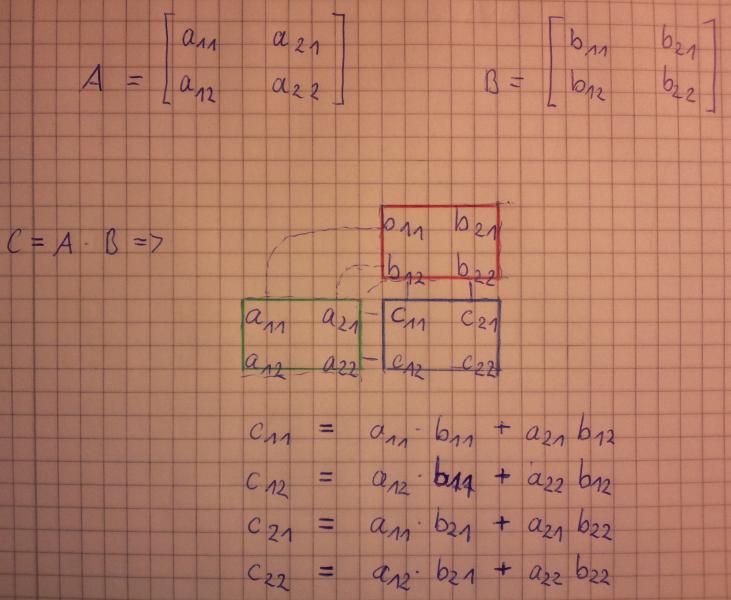
A =
 
[ 1 + 2*i, 3 - i]
[       5, 2 + i]
 
 
B =
 
[ - 2 + i,   4 + 2*i]
[      -1, - 7 - 3*i]
 
 
L1 = A*B =
 
[  - 7 - 2*i, - 24 + 8*i]
[ - 12 + 4*i,    9 - 3*i]
 
 
L2 = B*A =
 
[    16 + 7*i,    1 + 13*i]
[ - 36 - 17*i, - 14 - 12*i]

 

L3 = A+B =
 
[ - 1 + 3*i,     7 + i]
[         4, - 5 - 2*i]

 

b)

z_1,2 = sqrt(-24 -70i) = a +bi;

sqrt(-24 -70i) = a +bi;

-24 -70i = (a +bi)^2;

-24 -70i = a^2 -b^2 +2abi;

 

Koeffizientenvergleich:

I)  a^2 -b^2 = -24;

II) 2ab = -70;  --> b = -70/(2a);

a^2 -(-70/(2a))^2 = -24;

a^4 +24a^2 -1225 = 0;

Über Substitution t = a^2 und Resubstitution a = ±sqrt(t)

z₁=  5 -7i;

z₂= -5 +7i;

 

c)

einfach dreimal die Zahl mit sich selber multiplizieren

 

Comments

wie kommst du bitte auf "[  - 7 - 2*i, - 24 + 8*i] bei A*B ?

liebe grüße

---

i²= -1

2i² = 2(-1)

---

Muss man bei der c irgendwelche Potenzgesetze beachten wie z.B. die binom. Formeln oder sollte man sich eher auf das dreifache multiplizieren beschränken?

---

a⁴ +24a² -1225 = 0;

Subst.: t = a^2,

t^2 +24t -1225 = 0;

t_1,2 = -24/2 ±sqrt(24^2 +4*1225)/2;

t_1,2 = -12 ±sqrt(12^2 +1225);

t_1,2 = -12 ±sqrt(1369);

t_1,2 = -12 ±37;

t₁ = 25;

t₂ = -49;

Resubst. : a = ±sqrt(t)

a_1,2 = ±sqrt(t₁);

a₁ = 5;

a₂ = -5;

a_3,4 = ±sqrt(t₂);

a₃ = 7i;

a₄ = -7i;

Einsetzen in b =  -70/(2a):

b₁ = -70/(2a₁) = -7;

b₂ = -70/(2a₂) = 7;

b₃ = -70/(2a₃) = -70/(14i) = -70i/(14i^2) = 5i;

b₄ = -70/(2a₄) = -70/(-14i) = -70i/(-14i^2) = -5i;

Einsetzen in z_1,2 = sqrt(-24 -70i) = a +bi;

z1 = a₁ +b₁i = 5 -7i;

z2 = a₂ +b₂i = -5 +7i;

z3 = a₃ +b₃i = 7i +(5i)*i = -5 +7i;

z4 = a₄ +b₄i = -7i +(-5i)*i = 5 -7i;

Soweit so klar?  lg JR

---

A = [1+2*i, 3-i;
             5,  2+i]
B = [-2+i, 4+2*i;
          -1,  -7-3*i]

A*B = C;

c11 = (1+2*i)*(-2+i) + (-1)*(3-i) =
      = -2 -4*i +i -2 -3 +i = -7 -2i;

c12 = (5)*(-2+i) + (2+i)*(-1) =
      = -10 +5i -2 -i = -12 +4i;

c21 = (4+2*i)*(1+2*i) + (-7-3*i)*(3-i) =
      = 4 +2i +8i -4 -21 -9i +7i -3 = -24 +8i;

c22 = (4+2*i)*(5) + (-7-3*i)*(2+i) =
      = 20 +10i -14 -6i -7i +3 = 9 -3i;

C = [c11, c21;
       c12, c22];

---

Mach es so wie Du damit am besten zurecht kommst. Ich schreib es Dir mal mit der binomischen Formel auf, das dreifache Multiplizieren kannst Du ja selber ausprobieren:

-1/2 +sqrt(3)/2*i = a +b;

--> a = (-1/2);

--> b = (+sqrt(3)/2*i); //ja, das i gehört mit dazu. Ich schreib das erstmal so, um nicht immer -1/2 +sqrt(3)/2i schreiben zu müssen

(a +b)^3;

aus Pascalschem Dreieck die binomial Koeffizienten 1, 3, 3, 1 und a und b ersetzen

1*a^3*b^0 +3*a^2*b^1 +3*a^1*b^2 +1*a^0*b^3 =

= [sqrt(3)/2*i]^3 +3*(+sqrt(3)/2*i)^2*(-1/2) +3*(+sqrt(3)/2*i)*(-1/2)^2 +(-1/2)^3 =

= -3/8*sqrt(3)*i +9/8 +3/8*sqrt(3)*i -1/8 =

= 1;

Ich vermute mal, wenn Du weißt wie die binomischen Formeln aufgebaut sind ( https://de.wikipedia.org/wiki/Binomische_Formel#Verallgemeinerungen   und  https://de.wikipedia.org/wiki/Pascalsches_Dreieck), dann wirst Du damit schneller sein, weil Du dann nicht mehr so viel multiplizieren musst. Nur noch einsetzen, die Potenzen ausrechnen und addieren. Also in etwa die vier Zeilen, die ich gebraucht habe.

 

 

lg JR

---

Hier noch eine weitere Variante:

z = -1/2 +sqrt(3)/2*i = a +bi =A*exp(φ*i);

z^3 = A*exp(3*φ*i);

A = |a +bi| = sqrt(a^2 +b^2);

φ = arctan(b/a);

A = sqrt(1/4 +3/4) = 1;

φ = arctan(-sqrt(3)) = 120°;

z^3 = 1*exp(3*120°*i) =

= 1*cos(360°) +i*1*sin(360°) =

= 1 +0*i;

 

Das ist vermutlich die unkomplizierteste. Vorallem bei höheren Potenzen von z.

 

lg JR