gemeinsame koordinaten des gemeinsamen Punktes von t und n

Question

Gegeben ist die Funktion f mit f(x)=1/2x⁴ - x³ - 2; x∈R mit Schaubild K. t ist die Tangente an K in x=2, n ist die Normale von K in P(-1|f(-1)). Bestimmen Sie die Koordinaten des gemeinsamen Punktes von t und n. Fertigen Sie eine Skizze mit Tangente und Normale.

Answer 1

f(x) = 1/2x⁴ - x³ - 2

f '(x) = 2x³ - 3x² 

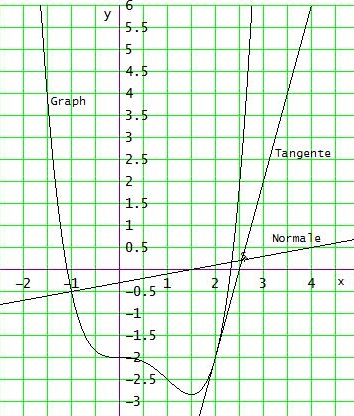
Tangente in B(2 | -2) hat die Steigung m_t = f '(2) = 4, 

Tangentengleichung:   y = 4 • (x - 2) - 2    ⇔  y =  4x - 10

Normale in (-1 | -1/2) ,  m_n = -1/f '(-1) = -1 / (-5)  = 1/5 

Normalengleichung:     y = 1/5 • (x + 1) - 1/2  ⇔  y = 1/5 x - 3/10

Gleichsetzen ergibt   x = 97/88  → y = 4/19   also  S( 97/88 | 4/19 )

 

Gruß Wolfgang