Gibt es a,b,c,d in R sd f nicht bijektiv ist?

Question

Seien a,b,c,d $\in \mathbb{K}$. Sei $f:\mathbb{K}^4\rightarrow\mathbb{K}^4$ die lineare Abbildung mit  Darstellungsmatrix

 

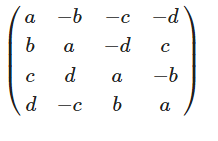
bezüglich der Standardbasis von $\mathbb{K}$.

Sei $\mathbb{K}=\mathbb{R}$.

Gibt es a,b,c,d $\in\mathbb{R}$ (nicht alle 0) sd. f nicht bijektiv ist?

Sei $\mathbb{K}=\mathbb{C}$.

Gibt es a,b,c,d $\in\mathbb{C}$ (nicht alle 0) sd. f nicht bijektiv ist?

Comments

Tipp: $\det M=(a^2+b^2+c^2+d^2)^2$.

---

dh det M muss gleich 0 sein damit es nicht bijektiv ist. Also gibt es

unendlich viele Lösungen denn a²+b²+c²+d² muss einfach 0 geben.

Was aber bei den komplexen Zahlen?

---

Im Fall $\mathbb K=\mathbb R$ existiert für $\det M=0$ nur die triviale Lösung $a=b=c=d=0$.
Im Fall $\mathbb K=\mathbb C$ wähle z.B. $a=1,b=i,c=d=0$.

---

Okay im ersten Fall habe ich es verstanden, wie kommst auf aber auf die Lösungen im zweiten Fall?

---

$1^2+i^2+0^2+0^2=1-1+0+0=0$.