Wieso ist das eine Gruppe? Ω = {1,2,....,d} ⊂ ℕ; Sd= {σ : Ω→Ω, σ ist bijektiv}. Operation: Hintereinaderausführen

Question

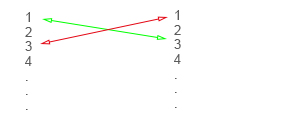
Sei Ω = {1,2,....,d} ⊂ ℕ und S_d= {σ : Ω→Ω, σ ist bijektiv}.

Mit der Hintereinanderausführung als Operation wird S_d zu einer Gruppe und heißt symmetrische Gruppe auf d Punkten.

Machen sie sich klar, dass es sich tatsächlich um eine Gruppe handelt!

 

So nun muss diese Menge mit der "Operation" ja nun : Assoziativ sein, Ein neutrales Element haben, und zu jedem Element muss ein Inverses existieren so dass a * 'a = n.

Für mich scheitert es doch schon an dem neutralen Element? oder wäre das id()?
Und dann ist da noch das Problem, der Hinterinanderausführung. 
Dreht man sich da nicht im kreis, aufgrund der Bijektivität, da aus dem grünen Pfeil der Rote folgt?

Ich hoffe mir kann das hier jemand erklären. Danke euch!

 

 

Answer 1

die Identität ist das neutrale Element und zu deiner Frage mit der Hintereinanderausführung. Vielleicht hilft dir ein kleines Gegenbeispiel, dass nicht aussieht wie dein Beispiel oben und trotzdem bijektiv ist.

angenommen du hast folgende Abbildungsvorschrift:

1->2

2->3

3->4

...
d->1

Dann ist die Abbildung trotzdem bijektiv, aber wenn du diese Vorschrift 2 mal hintereinander ausführst, hast du trotzdem nicht das Problem, dass du dich im Kreis drehst ;)

Ich hoffe ich konnt dir helfen