Suche maximalen Definitionsbereich DMAX. (a) f(x)=(x2-1/4x)/(-x2+4x√(x)+1/4x-√(x)); (b) g(x)=exp(-1/(In(x)-1))

Question

Ermitteln Sie auch das Verhalten an den Rändern des Denitionsbereichs und geben Sie, wenn möglich, eine stetige Fortsetzung auf einen größeren Bereich an.

(a) f(x)=(x²-1/4x)/(-x²+4x√(x)+1/4x-√(x))

 

(b) g(x)=exp(-1/(In(x)-1))

 

Ich brauche beide Lösungswege zu vergleichen. Bei (b) weis ich nicht wie ich anfangen soll.

Comments

@Anonym: Ich habe in der Überschrift eine schliessende Klammer im Nenner ergänzt. Ist sie am richtigen Ort.

---

Jop, danke, ich habe es übersehen.

---

Vielleicht kannst du den Angaben im Link zu (a) entnehmen, wie man den nenner faktorisieren könnte.

https://www.wolframalpha.com/input/?i=f%28x%29%3D%28x%5E2-1%2F4x%29%…

'Domain' ist übrigens der Definitionsbereich.

---

Hmmmm, verstehe nicht wie er auf diese kommt. Kann man an diese Programme anschauen was die gemacht hat?

---

wie rechnet man aus mit d/dx? Wie lautet dort die Formel?

---

d/dx ist die Ableitung. Die brauchst du aber nicht für deine Frage.

Answer 1

(x² - 1/4·x)/(- x² + 4·x·√x + 1/4·x - √x)

Nenner darf nicht Null sein

- x² + 4·x·√x + 1/4·x - √x ≠ 0
- x² + 4·x^3/2 + x/4 - √x = 0  

Substitution x = z²

- z⁴ + 4·z³ + 1/4·z² - z = 0

Wir finden zwei ganzzahlige Nullstellen für z = 4 ∨ z = 0

Nach polynomdivision und abc-Formel noch die Nullstellen z = - 1/2 ∨ z = 1/2

Ich bestimme x

x1 = 0² = 0
x2 = 4² = 16
x3 = (1/2)² = 1/4

D = R \ {0, 0.25, 16}

 

(x² - 1/4·x)/(- x² + 4·x·√x + 1/4·x - √x)

Substitution x = z²

(z⁴ - 1/4·z²) / (- z⁴ + 4·z³ + 1/4·z² - z)
z²*(z² - 1/4) / (-z*(z - 4)*(z + 1/2)*(z - 1/2))
z²*(z + 1/2)*(z - 1/2) / (-z*(z - 4)*(z + 1/2)*(z - 1/2))

Kürzen

z / (-(z - 4))
z / (4 - z)

Polynomdivision

z : (4 - z) = -1 + 4 / (4 - z)

Resubstitution z = √x

-1 + 4 / (4 - √x)

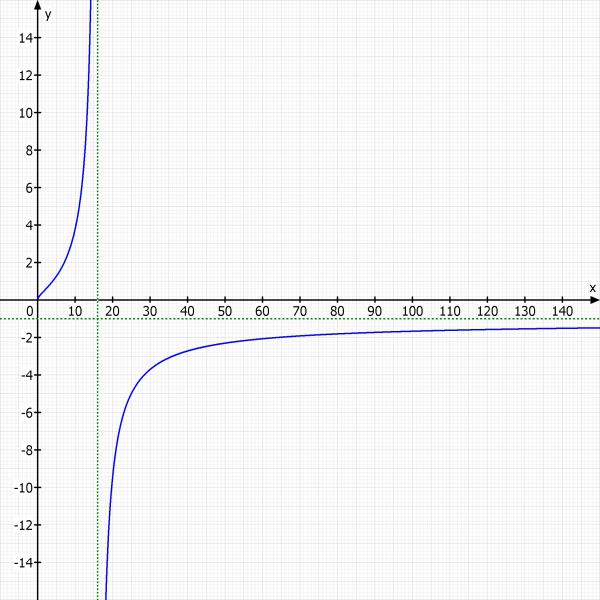
Das ist also unsere Stetig ergänzte Funktion. Asymptote für x → ∞ ist hier -1. Polstelle haben wir bei 16.

Ich mache dir noch eine Skizze

Comments

f(x) = e^{- 1/(LN(x) - 1)} = e^{1/(1 - LN(x))}

aus ln(x) → x > 0

1 - ln(x) ≠ 0
x ≠ e

D = R⁺ \ {e}

lim _{x → 0⁺} f(x) = 1

lim _{x → e^-} f(x) = ∞

lim _{x → e⁺} f(x) = 0

lim _x → ∞ f(x) = 1

Skizze