dein Baumdiagramm ist nicht richtig angelegt, die Zahl n=6 spielt nur bei der Anzahl der Stufen des Baumdiagramms eine Rolle:
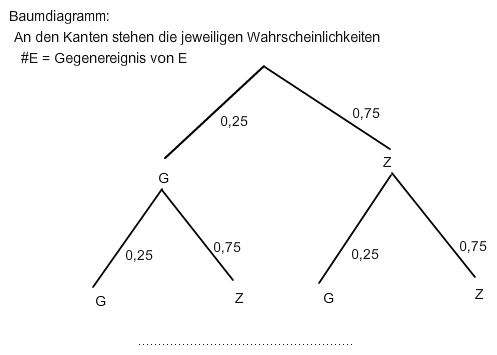
[ #E spielt hier keine Rolle]
a)
P("nur Tiere mit glattem Fell") = 0,256 ≈ 0,000244 = 0,024 %
b)
Bei Einem Zufallsexperiment mit genau 2 möglichen Ergebnissen mit den Wahrscheinlichkeiten p (für "Treffer") und 1-p (für "Niete") beträgt - wenn man es n-mal durchführt - die Wahrscheinlichheit für genau k Treffer:
P( T= k ) = \(\begin{pmatrix} n \\ k \end{pmatrix}\)· pk · (1-p)n-k
Sei T = ("glattes Fell") , p = 0,25 , n = 6
P(T=1) = \(\begin{pmatrix} 6 \\ 1 \end{pmatrix}\) * 0,251 * 0,755 ≈ 0,297 = 29,7%
c)
P(T≥2) = 1 - P(T=0) - P(T=1) ≈ 0,466 = 46,6 %
d)
Erwartungswert = 6 * 0,25 = 1,5
(Man erwartet also 1 oder 2 Tiere mit glattem Fell)
Gruß Wolfgang