Wie Definitionsbereich zeichnen?

Question

Aufgabe:

fi: Dfi → Wfi, Dfi ⊂ \( ℝ^{2} \), Wfi ⊂, i =3,4 der Gestalt

f1(x,y)= ln(\( \sqrt{x^2+y^2} \)), f2(x,y) = arctan (\( \frac{y}{x} \))

a.)Best und skizzieren des grösstmöglichen Df. Für jede Funktion Wertebereich angeben

Hat jemand eine Idee oder könnte mir kurz zeigen, wie man das anschaulich zeichnen könnte ?

Comments

Zunächst musst Du den Definitionsbereich bestimmen- also prüfen, für welche x,y die Funktionswerte berechnet werden können.

---

Df 3= R^2

Wf=R

f4 Df R^2

Wf von -pie bis pie

Wie zeichnet man das aber ?

---

Was ist denn \(\ln(0)\)? Und wer teilt bitte durch 0?

Teilmengen des \(\mathbb{R}^2\) kannst du in einem Koordinatensystem skizzieren.

---

Geh von innen nach außen und überlege, wann der Ausdruck existiert.

Erste Funktion: x² existiert offensichtlich für jedes x (analog y). Die Summe existiert auch immer. Die Wurzel existiert nur, wenn der Radikand nicht-negativ ist - was hier der Fall ist da Quadrate immer nicht-negativ sind.

Der Logarithmus existiert nur für positive Argumente. Die Wurzel liefert nur positive Werte - außer der Radikand ist Null. Das ist also die erste Einschränkung. Wann wird der Radikand Null? Nur wenn x und y Null sind.

Damit haben wir den maximalen Definitionsbereich, alle x,y sind erlaubt außer x=y=0

Zeichnerisch würde man die x,y Ebene zeichnen und den Ursprung als ausgeschlossen markieren.

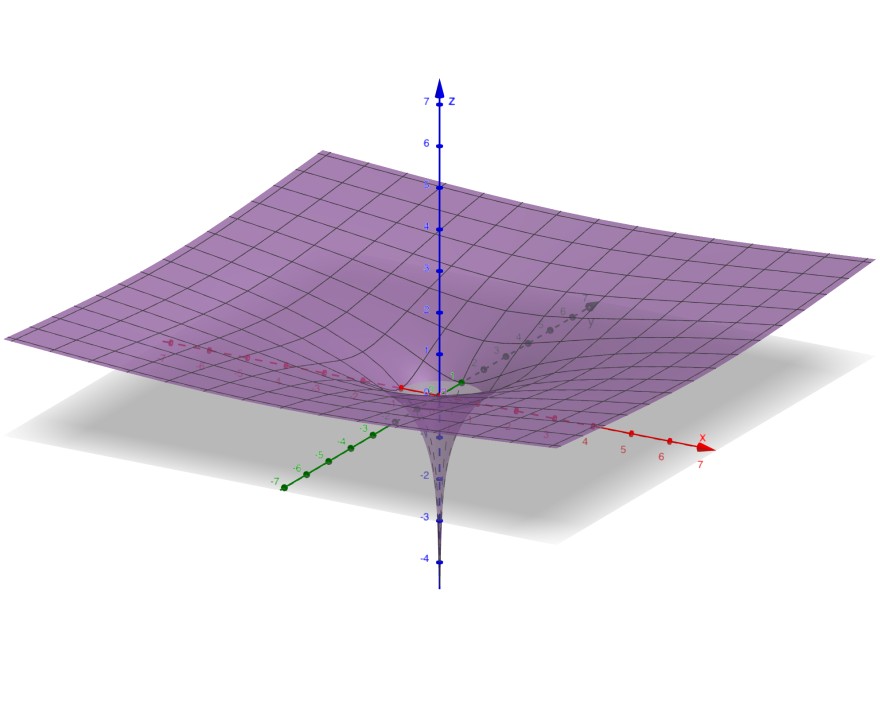
Sieht übrigens witzig aus die Funktion: