Monotonie von x^4*e^{-2x}

Question

Hallo

Wie kann ich die monoton wachsenden Intervalle von dieser Funktion  bestimmen

y=x^4*e^{-2x}.

e^{-2x} ist doch immer positiv??

Answer 1

Hallo

du musst feststellen, in welchen Intervallen die Steigung f ' positiv (negatv) ist. Dazu brauchst du die Nullstellen von f ' :

Die Produktregel [ u * v ] ' = u' * v + u * v ' ergibt

f '(x) = 4x³ * e^-2x + x⁴ * (-2) * e^-2x  =  4x³ * e^-2x - 2x⁴ * e^-2x

2x³ * e^-2x ausklammern

f '(x) = 2·x³ · e^-2x · (2 - x)  = 0

  →  x₁ = 0 ; x₂ = 2  jeweils mit Vorzeichenwechsel  (VZW)

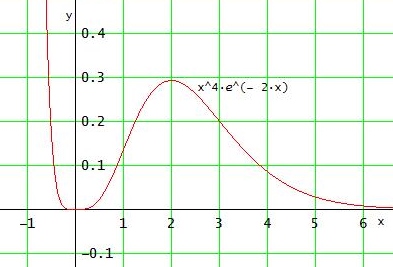
Monotonieintervalle von f:

] - ∞ ; 0 ]   streng monoton fallend , da  f ' (-1) < 0

[ 0 ; 2 ]   streng monoton steigend , wegen VZW von f '

[ 0 ; ∞ [   streng monoton fallend    , wegen VZW von f '

Gruß Wolfgang