normale Winkelberechnung 8. Nr. 47.

Question

Dies ist die letzte Aufgabe. Wie imemr das gleiche Proble.

Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.1.47, ISBN 3-12-722310-2, 1981, S. 9

Comments

Vom Duplikat:

Titel: Eigenmann: Nummer 47, Teil 1

Stichworte: geometrie,eigenmann,eigenmann-1-1,kreiswinkelsatz

Aufgabe:

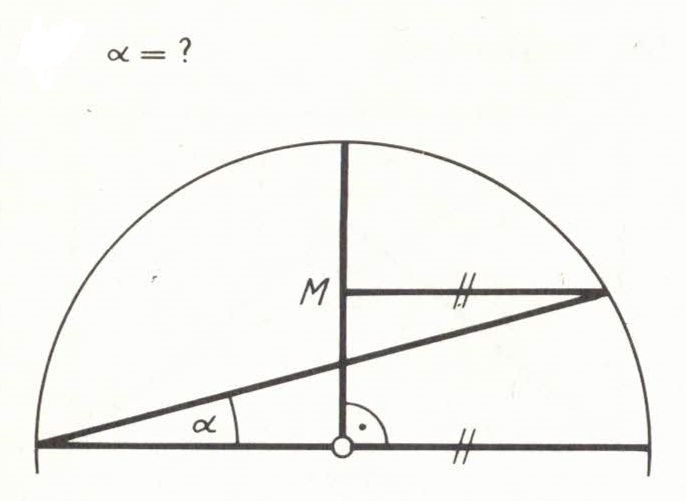
Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.1.47, ISBN 3-12-722310-2, 1981, S. 9

Problem/Ansatz:

Der Winkel ist Teil eines rechtwinkligen Dreiecks (Halbkreis des Thales). Dessen Höhe ist 1/4 des Kreisdurchmessers, sodass man mit trigon. Rechnungen zu α = 15° findet. Nach Rechnen mit irrationalen Zahlen entsteht schlussendlich mit 15 eine rarionale Zahl. Also gibt es einen eleganteren Lösungsweg. Welchen?

Mit trigonometrischen Rechnungen

---

Wenn der Urprung Mittelpunkt eines Kreises mit Radius = 2 ist, dann folgt aus der Kreisgleichung

\(\displaystyle (x-0)^{2}+(1-0)^{2}=2^{2} \)

dass \(\displaystyle P\left(\sqrt{3} \; \vert \; 1 \right) \)

und

\(\displaystyle \alpha = \text{arccot}(2+\sqrt{3}) = \frac{\pi}{12} = 15^{\circ} \)

Hier breitet ein deutscher Jungfilmer seine Gedanken zu diesem Problem aus: >> klick <<

---

döschwo

aus der Kreisgleichung

Danke.

Ich muss aber staunen, dass der Taschenrechner (TI-30XIIS), nachdem er unter Beteiligung einer irrationalen Zahl (1,732 .....) wieder zu einer rationalen findet (15).

---

Wenn man annimmt, das Argument habe der TR ungenau mit

\( \underbrace{3,732050808}_{\text{10 Stellen}} \)

und die arccot-Funktion genau, dann gibt es

\( \underbrace{14,99999999}_{\text{10 Stellen}}83... \) Grad, was er dann wieder auf 15 gerundet hat.

Man könnte auch einen TR wie den SwissMicro DM32 oder R47 verwenden, der hat 34 Stellen in der Mantisse, und rechnet sogar mit Schweizer Elektronen.

Aber die Idee vom Mathecoach mit dem Kreiswinkelsatz verhindert solche Probleme ja gänzlich. Und die Aufgabe ist ohne Taschenrechner.

Answer 1

wenn M der Mittelpunkt der senkrechten Linie ist, dann sei r der Radius des Kreises, M_k dessen Mittelpunkt und P der rechte Kreispunkt, wo sich drei Linien schneiden.

Dann gilt im rechtwinkligen ΔM_kMP:

∠ MPM_k = 2α    (zu dem von dir markierten Teilwinkel α kommt noch einmal der Stufenwinkel der Größe α hinzu)

sin(2α) =  (r/2) / r  = 1/2

→  2α = 30°  →  α = 15°

Gruß Wolfgang

Comments

Ich gebe mal ein Daumen Hoch,

Ich selber hatte nur keine Lust zu Antworten weil von Fragesteller vermutlich eh nicht mal ein Danke kommt.

---

Dafür kommt von mir ein "Danke" für den Daumen :-) - und den interessanten Hinweis, dass er nicht vom Fragesteller kommt.

---

Von mir auch gerade ein Daumen ;)

Mir gefallen diese Fragen. Ich wollte aber erst mal sicherstellen, dass da nicht mehrmals das gleiche Bild hochgeladen wurde, und habe angefangen die Überschriften mit den Fragenummern in den Bildern zu versehen. (bisher habe ich kein Duplikat entdeckt)

---

Hallo Lu,

danke dir :-) , mir gefallen die Aufgaben auch. Man könnte den Eindruck haben, dass Silverdart gerade an einem Lösungsbuch schreibt  und deshalb keine Zeit für abschließende Kommentare hat :-)

---

Vielleicht kann Silverdart ja mal mitteilen aus welchem Fundus diese Aufgaben stammen. Sieht so aus als habe sich da ein Lehrer sehr viel Mühe gegeben.

---

Ich schreibe normalerweise immer unter den Fragen vielen Dank.., jeder sollte wissen, dass das eine sehr grosse Hilfe ist für Schüler, die eine Prüfung haben und deswegen ihre Aufgaben lösen. Ich löse gerade ca. 50 Aufgaben und kann halt manchmal nicht immer die ganzen Sätze in den Fragen schrieben.

Diese Aufgaben sind "Eigenmann" Aufgaben, so nennt sie unsere Lehrerin.

---

Hallo, ich verstehe nicht, wie man von 2*Alpha = 30° kommt?

Die Rechnung lautet ja 2*Alpha + ? + 90° = 180° und das ? wäre 60°, aber ich verstehe nicht, wie man auf 60° kommt.

Vielen Dank im Voraus!

---

ich verstehe nicht, wie man von 2*Alpha = 30° kommt

Da wir nur von einem spitzen Winkel α reden:

sin(30°) = 1/2    das ist einfach so

sin(2α) = 1/2     wurde in der Antwort erklärt

→  2α = 30°  

---

2*Alpha + ? + 90° = 180° und das ? wäre 60°, aber ich verstehe nicht, wie man auf 60° kommt.

Dein Winkel ? kommt ja in meiner Rechnung für α = 15° nicht vor.

Wenn du α =15° glaubst, ergibt sich doch automatisch ? = 60°

---

@Lu, @-Wolfgang-, @der_Mathecoach

Sehe gerade, dass nach 8 Jahren immer noch die Aufgaben gelöst werden. Mittlerweile habe ich meinen Bachelor (Technisch). Das war aber noch 2-3 Jahre davor.

Habe auch gesehen, dass ich mich damals nicht aufrichtig bedankt habe. Habe dieses Thema gehasst . Jedoch bedanke ich mich jetzt, ihr habt mir sehr geholfen während dieser Zeit die Aufgaben zu lösen!

---

Nett von dir!

Gehe hin in Frieden :-)

Answer 2

Beachte immer die Hinweise von Eigenmann. Die Aufgaben sind nicht ohne Grund in Paketen angeordnet.

Es gilt sin(30°) = 0.5 und damit

Answer 3

Du solltest noch dazu sagen, dass M Mittelpunkt der Strecke ist, und die beiden Doppelstriche Parallelität bedeuten (steht im Buch vorne im Vorwort). Das mit den Doppelstrichen sollte schon deshalb erwähnt werden, weil Doppel-- oder Dreifachstriche normalerweise für gleiche Längen stehen. Außerdem ergibt sich die Parallelität hier zwangsweise wegen der beiden rechten Winkel.

Vom Kreismittelpunkt ausgehend hast Du nach links, oben, rechts und schräg jeweils den Radius r. Vom rechten Punkt nach oben ist eine Linie bereits angedeutet, die bildet ein gleichseitiges Dreieck. Damit ergibt sich für das gesuchte Dreieck:

alpha+alpha+60+90 = 180.

Grüße,

M.B.

Comments

Hallo, ich verstehe nicht, wie man von 2*Alpha = 30° kommt?

Die Rechnung lautet ja 2*Alpha + ? + 90° = 180° und das ? wäre 60°, aber ich verstehe nicht, wie man auf 60° kommt.

Vielen Dank im Voraus!

---

2*Alpha

ist die Größe eines Außenwinkels eines Dreiecks, in dem zwei (diesem Außenwinkel NICHT anliegende) Innenwinkel jeweils die Größe  α haben.

https://de.wikipedia.org/wiki/Außenwinkelsatz

---

Ich habe den Punkt mit 2*Alpha verstanden, nur komme ich nicht drauf, wie man auf die 60° kommt, also wie ich was rechnen muss.