fx'(1.9, 1.9) = 1295.859895
fy'(1.9, 1.9) = 1170.116086
Veränderung
0.9 * 1295.859895 - 0.2 * 1170.116086 = 932.2506883
Genaue Rechnung
f(1.9 + 0.9, 1.9 - 0.2) - f(1.9, 1.9) = 2637.542006
Oh weh. Das ist hier ja eine ganz schöne Abweichung.
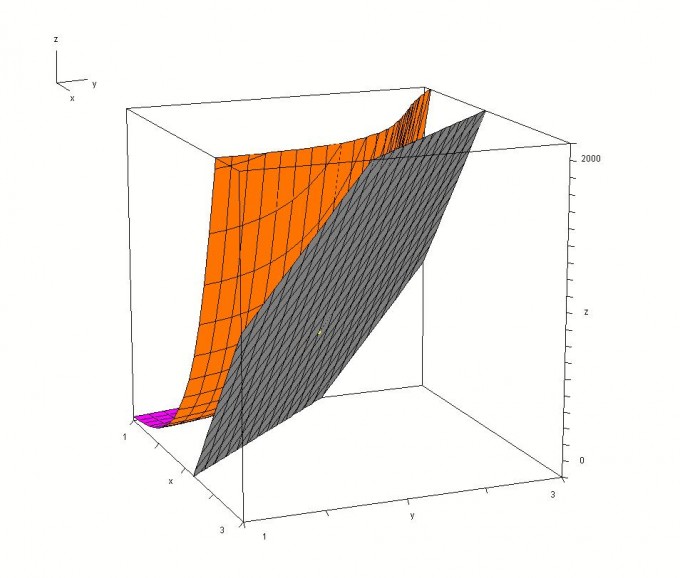
Die Skizze verdeutlicht das