In diesem Fall ist es sehr einfach, da die Punkte A und C symmetrisch zur Senkrechten durch B liegen. Damit ist B der Scheitelpunkt der Parabel wie hier zu sehen ist:
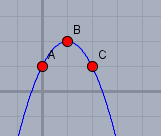
Mit etwas Erfahrung lässt sich sofort die Scheitelpunktform der Parabel hinschreiben: $$f(x)=-(x-1)^2+2=-x^2+2x+1$$
Im Allgemeinen löst man dies über Einsetzen in die von Dir bereits erwähnte allgemeine Form \(f(x)=a_2 x^2 + a_1 x + a_0\). Dann erhält man $$a_2 \cdot 0^2 + a_1 \cdot 0 + a_0 = 1 \quad \Rightarrow a_0=1$$ $$a_2 \cdot 1^2 + a_1 \cdot 1 + a_0=2$$ $$a_2 \cdot 2^2 + a_1 \cdot 2 + a_0 = 1 $$ Aus der zweiten Gleichung folgt dann, dass \(a_1=1-a_2\) und wenn man dies in die dritte einsetzt, so erhält man \(4a_2 + 2(1-a_2) + 1 = 1\) bzw. \(a_2=-1\). Ist natürlich das gleiche Ergebnis: $$f(x)=(-1)x^2 + 2x +1$$ Gruß Werner