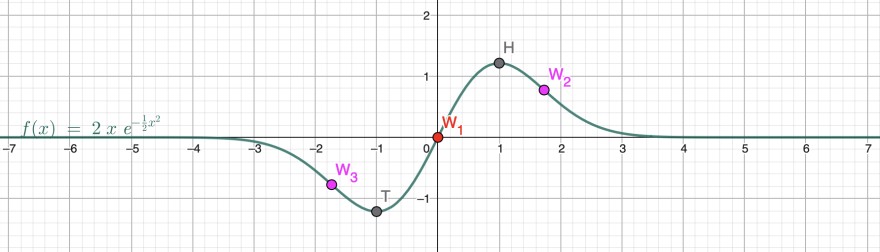
\( f(x)=2x e^{-1/2x^2} \) Kurvendiskussion:
Nullstellen:
\( f(x)=2x e^{-1/2x^2}=0 \) Satz vom Nullprodukt:
\(2x =0 \).
\(x =0 \).
\( e^{-1/2x^2}=0 \) kann nicht Null werden.
Extrema:
\( f'(x)=2e^{-1/2x^2} +2xe^{-1/2x^2}(-x)=e^{-1/2x^2} (2-2x^2)\)
\( e^{-1/2x^2} (2-2x^2)=0\)
\( 2-2x^2=0\)
\( x_1=1\) \( f(1)=2 e^{-1/2} =\frac{2}{\sqrt{e}}\)
\( x_2=-1\) \( f(-1)=-2 e^{-1/2} =-\frac{2}{\sqrt{e}}\)
Art der Extrema:
\( f''(x)=e^{-1/2x^2}(-x) (2-2x^2)+e^{-1/2x^2}(-4x) \)
\( f''(1)=e^{-1/2}(-1) (2-2)+e^{-1/2}(-4)<0 \)Maximum
\( f''(-1)=e^{-1/2}(1) (2-2)+e^{-1/2}(4) >0\) Minimum
H\( (1|\frac{2}{\sqrt{e}})\)
T\( (-1|\frac{2}{-\sqrt{e}})\)
Wendepunkte:
\( e^{-1/2x^2}(-x) (2-2x^2)+e^{-1/2x^2}(-4x)=0 \)
\( e^{-1/2x^2}(2x^3-6x)=0 \)
\( 2x^3-6x=0 \)→ \( x(x^2-3)=0 \)
\(x_1=0 \) ist schon Nullstelle
Bei den Extrema erscheint es nicht. Steigung berechnen:
\( f'(0)=2\) Falls der Wert 0 ist, liegt ein Sattelpunkt vor.
\( x_2=\sqrt{3}\) \( f(\sqrt{3})=2\sqrt{3} e^{-\frac{3}{2}} \)
\( x_3=-\sqrt{3}\) \( f(-\sqrt{3})=-2\sqrt{3} e^{-\frac{3}{2}}\)
\(W_2( \sqrt{3}|2\sqrt{3} e^{-\frac{3}{2}}) \)
\(W_3( -\sqrt{3}|-2\sqrt{3} e^{-\frac{3}{2}}) \)
Symmetrieeigenschaft:
Punktsymmetrie zum Ursprung liegt dann vor, wenn\( f(-x)=-f(x) \)
\( f(-x)=-2x e^{-1/2x^2}\)
\( -f(x)=-2x e^{-1/2x^2}\) Somit punktsymmetrisch zum Ursprung.
Globalverhalten:
\( \lim\limits_{x\to\infty}2x e^{-1/2x^2}= \lim\limits_{x\to\infty}\frac{2x}{e^{1/2x^2}}\)→ 0
\( \lim\limits_{x\to-\infty}2x e^{-1/2x^2}= \lim\limits_{x\to-\infty}\frac{2x}{e^{1/2x^2}}\)→0