Vektoren (Abstand Punkt- Ebene). Rechtwinkliges Dreieck und a^2+b^2=c^2 und Umkehrung zeigen.

Question

a) Beweise Den Satz Des Pythagoras ( in einem rechtwinkligen Dreieck gilt a^2+b^2= c^2, indem du die Seiten eines rechtwinkligen Dreiecks durch die Vektoren a,b und c darstellen..

b) Beweise ebenfalls vektoriell die Umkehrung des Satzes; gilt in einem Dreieck a^2+b^2=c^2, dann liegt zwischen den Seiten a und b ein rechter Winkel.

Answer 1

Hallo IA,

im Bild ist geometrisch die Summe zweier Vektoren \(\vec{a}\) und \(\vec{b}\)  dargestellt:

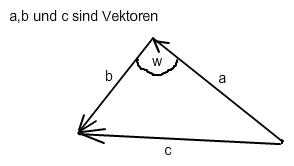
Im Bild gilt (unabhängig von der Größe von Winkel w)

\(\vec{c}\) = \(\vec{a}\) + \(\vec{b}\)     (1)

Für jeden Vektor \(\vec{x}\) gilt  |\(\vec{x}\)|² = \(\vec{x}\)²   (2)  

Für zwei Vektoren gilt:    \(\vec{x}\) ⊥ \(\vec{y}\)  ⇔  \(\vec{x}\) * \(\vec{y}\)  = 0      (3)

Die Länge einer Seite ist jeweils der Betrag des Vektors.

a)   Satz von Pythagoras

Voraussetzung:   w = 90°   (Dreieck ist rechtwinklig)

Behauptung:   |\(\vec{c}\)|² = |\(\vec{a}\)|² + |\(\vec{b}\)|²  

Beweis:  Es gilt

 |\(\vec{c}\)|²  =₍₂₎   \(\vec{c}\)²  =₍₁₎  ( \(\vec{a}\) + \(\vec{b}\) )² =  \(\vec{a}\)² + 2* \(\vec{a}\) * \(\vec{b}\) + \(\vec{b}\)²   (1. binomische Formel)

                     =₍₃₎   \(\vec{a}\)² +  0  + \(\vec{b}\)² =₍₂₎  |\(\vec{a}\)|² + |\(\vec{b}\)|²  

b)  Kehrsatz

Voraussetzung:    |\(\vec{c}\)|² = |\(\vec{a}\)|² + |\(\vec{b}\)|²  

Behauptung:  w = 90°   (Dreieck ist rechtwinklig)

Beweis:  Es gilt

 |\(\vec{c}\)|² =₍₂₎  \(\vec{c}\)²  =₍₁₎  ( \(\vec{a}\) + \(\vec{b}\) )² =  \(\vec{a}\)² + 2* \(\vec{a}\) * \(\vec{b}\) + \(\vec{b}\)² =₍₂₎  |\(\vec{a}\)|² + 2* \(\vec{a}\) * \(\vec{b}\) + |\(\vec{b}\)|² 

 Nach Voraussetzung gilt aber  |\(\vec{c}\)|² = |\(\vec{a}\)|² + |\(\vec{b}\)|²  

→  \(\vec{a}\) * \(\vec{b}\)  = 0   →₍₃₎   w = 90°   

Gruß Wolfgang