Hallo Sonnenblume,
du liegst wohl richtig:
es ist über dem Intervall [ π/3 ; π ] der Flächeninhalt zwischen den Graphen
f(x) = x2 * sin(x) und g(x) = -1 zu berechnen.
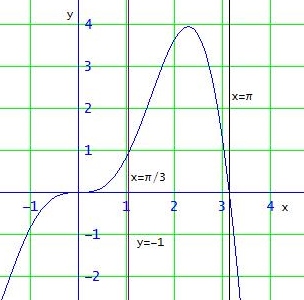
Für die Vorgehensweise (auch für deine) ist es wichtig, dass f(x) in [ π/3 ; π ] keine Nullstellen hat
( weil x2 * sin(x) > 0 ⇔ sin(x) > 0 , was in [ π/3 ; π ] erfüllt ist )
Die Graphen von f und g haben also keine Schnittstellen in [ π/3 ; π ]
und Gf verläuft oberhalb von Gg
A = π/3∫π ( f(x) - g(x) ) dx = π/3∫π ( x2 * sin(x) + 1 ) dx
= [ (2 - x^2)·COS(x) + 2·x·SIN(x) + x ]π/3π
≈ 11.01119705 - 7.698511491 ≈ 7.698511491
Gruß Wolfgang