
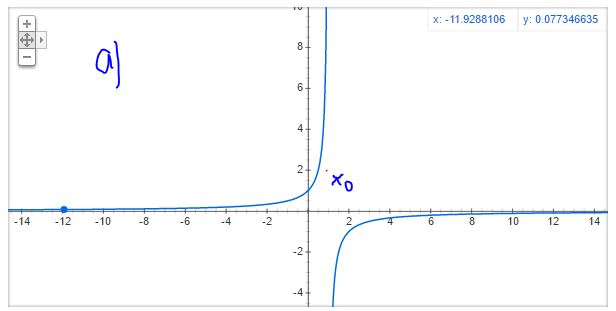
Stecke bei Aufgabenteil b) total fest. Wenn ich den Graphen zeichne ist es offensichtlich, dass es einen Sprung gibt, allerdings schaffe ich es einfach nicht, ein vernünftiges x zu finden, so dass gilt:
|x-1|<δ und
|1/(1-x)-2|>=ϵ
Dachte daran für x=(δ/2)+1 zu wählen, komm dann aber bei der zweiten Ungleichung nicht weiter.
ϵ sollte in diesem Fall doch beliebig groß werden können, da beide Kurven bei x0 nach jeweils +unendlich und -unendlich streben?
Beweisen Sie mit ϵ und δ, dass f nicht stetig in 1 ist. f(x):=1/(1-x) falls x≠1 , f(1):=a